Měření stromů a informací

Co se naučíš:

• Spočítat, kolik možností lze rozlišit pomocí daného počtu otázek a naopak.
• Posoudit vzájemnou nezávislost zpráv.
• Jak se měří informace a proč právě tak.
• V jakých jednotkách se informace měří, co je to jeden bit informace.
• Spočítat množství informace v dané zprávě.

Obvyklý průběh hodiny a metodické poznámky

Návrh průběhu hodiny a metodické poznámky

• Stručný průběh a poznámky
• [[[:Archiv:Učebnice/Informace/Měření stromů a informací/Hodina/PRIM-UL]] Podrobný plán (příprava do hodiny)]

Šťastný a spokojený život lze bezpochyby žít i bez znalosti odvození měření informace. Kdybychom ale výsledné závěry předložili jako „spadlé z nebe“ k uvěření, zůstal by zvídavý student nespokojen. Hledání vhodné míry (s předem danými vlastnostmi) pro nějakou veličinu je přitom poměrně neobvyklá, ale o to zajímavější úloha. Proto jsme sepsali toto poměrně přirozené odvození.

Někteří studenti ovšem až tak zvídaví nejsou. Volíme tedy podle jejich úrovně a zájmu:

Můžeme sledovat úplný postup popsaný zde v učebnici. 

Je třeba věnovat zvýšenou pozornost tomu, aby studenti po celou dobu chápali, co děláme a co tím sledujeme. Stejně tak důležité je dobré porozumění předchozí látce, které úvahy velmi usnadní. Není smyslem (a nelze vyžadovat!), aby si studenti odvození zapamatovali. Tak jako i v jiných předmětech, cílem zde je zprostředkovat vhodně zjednodušený myšlenkový proces, kterým informatik dojde k výsledku (resp. kdysi k němu mohl podobně dojít). Pamatovat si studenti budou výsledné poznatky a zkušenost, že je odvodit lze.

Pracujeme s příkladem o neznámé denní době, což je pro studenty přístupná situace, zároveň ale dost bohatá na různé zprávy. Zformulujeme požadavky na „měřítko“ informace a snažíme se hledat, co by požadavkům vyhovělo. Zásadní je požadavek na sčítání množství informace v nezávislých zprávách. Právě ten vede jak v naší zjednodušené školní situaci, tak i ve skutečném odvození s entropií, k použití logaritmu. Postupně prozkoumáme několik možností, jak by snad šlo informaci měřit (počet vyloučených možností, poměr vyloučených možností, počet ušetřených otázek). Pro první dvě najdeme příklady, které porušují naše požadavky. Teprve ušetřené otázky fungují podle očekávání.

Ušetřené otázky jsou zároveň už převlečený logaritmus. To je pro studenty zpravidla obtížné téma. I proto kolem něj kroužíme delší dobu (např. zkoumáním vztahu počtu odpovědí a rozlišených možností na začátku hodiny).

Nebo můžeme obtížnější pasáže přeskočit (a případně se k nim vrátit později).

V následujících odstavcích popsaný průběh hodiny a plán podle projektu PRIM (viz odkaz výše) odpovídají právě tomuto jednoduššímu a zároveň zcela dostačujícímu průchodu, určenému všem středoškolákům. Některé dílčí kroky jsou uvedeny jako fakta, nevyužíváme logaritmus (ovšem pokud jej studenti znají a chápou, souvislost samozřejmě využijeme!). Místo toho pracujeme s počtem ušetřených otázek.

Jmenovitě: Zastavíme se před příkladem s nezávislými zprávami (pojem nezávislosti nezavádíme) a zcela vynecháme oddíly “Požadované vlastnosti měřítka na informace”, “Jak změřit, kolik toho nevíme?“ a “Přesné měření”. Studenti by měli rozumět zelenému shrnutí na konci kapitoly.

V každém případě zde pro většinu studentů vrcholí cesta k měření informace.

Prvním krokem je zjištění, že mezi počtem možností a počtem otázek potřebných k určení jedné z nich je úzký vztah. Mnohé žáky (zejm. ty, kteří očekávají přímou úměru) překvapí, jak rychle roste rozdíl mezi oběma veličinami: pro 1000 možností stačí 10 otázek, se 20 otázkami rozlišíme možností milion.

Následně už lze uvažovat, jak vlastně měřit množství informace. Studenti už vědí, že jde o vyloučené možnosti. Porovnávat ale přímo jejich počet nám příliš nepomůže. Studenti snadno najdou případy, kdy bychom dostali absurdní výsledky. Nejlepší smysl koneckonců dává, aby každá optimálně "půlící" otázka dávala informace stejné množství, bez ohledu na to, jestli na polovinu dělí 256 nebo 4 možnosti.

Pro pouhé porovnání informace obsažené v nějakých zprávách lze počítat poměr vyloučených a všech možností: čím vyšší poměr, tím více informace zpráva nese. Vidíme také, že velmi záleží na tom, co už víme (s kolika a kterými možnostmi aktuálně pracujeme).

Pokud chceme množství informace vyčíslit, potřebujeme jít ještě o krok dál. Snažíme se najít způsob, který by odpovídal intuici, že množství informace odpovídá tomu, kolik jsme se dozvěděli. Tedy rozdílu mezi tím, kolik víme po přijetí informace a kolik před tím. A my už máme jedno vcelku použitelné měřítko toho, kolik o něčem (ne)víme: počet otázek, které bychom museli položit, abychom vyloučili všechny možnosti kromě té správné. Množství informace ve zprávě tak můžeme vyjádřit jako počet otázek, které nám daná informace ušetřila. Tyto úvahy se vyplatí ukazovat přímo na nějakém rozhodovacím stromě.

Abychom např. určili jedno číslo ze 32, budeme potřebovat 5 otázek. Pokud nám někdo sdělí, že je hledané číslo násobkem 4, vyloučí tím 3/4 možností a ponechá 8. Pro určení jedné možnosti z 8 potřebujeme 3 otázky. Zpráva nám tedy dvě otázky ušetřila. Obsahovala dvě "jednotky" informace.

Pro úplnost doplníme, že základní jednotkou množství informace je bit. Odpovídá právě vyloučení poloviny možností, neboli odpovědi na jednu půlící otázku. Takovou odpověď lze zaznamenat jednou ze dvou možných hodnot, tradičně 0 a 1. Odtud slovo bit (binary digit).

Tento výklad by díky předchozím zkušenostem pro žáky poměrně přirozený, a s pomocí příkladů a rozhodovacích stromů také dostatečně názorný. Dohromady nejde o téměř nic vyloženě nového, spíše jde o uspořádání známých pozorování a uvedení několika souvislostí.

Hodinu uzavřeme procvičováním.

Další poznámky

• Ani zde samozřejmě není nutné postupovat přesně podle popisu. Studenti mohou např. něco přeskočit jako triviální poznatek nebo něco sami objeví, ale v nečekaném pořadí. V takovém případě nemá smysl jim bránit a snažit se je vrátit na „správnou cestu“.
• Veškeré počítání v průběhu hodiny si lze samozřejmě ulehčit použitím počítačů. Přinejmenším ukázkové a celočíselné výpočty doporučujeme provádět ručně, aby studenti mohli lépe sledovat, co se děje.
• Počítání množství informace přes počet ušetřených otázek není zcela přesné, může se až o jeden bit lišit. Komu ze studentů to vadí, naučí se ty logaritmy, aby mohl počítat přesně.

V téhle kapitole odhalíš několik nejdůležitějších poznatků teorie informace. Na základě předchozích příprav se konečně dobereme toho, jak vlastně množství informace měřit. Nejdřív si rozmyslíme, jaké od měření informace očekáváme vlastnosti. Následně s pomocí příkladu na určováním denní doby prozkoumáme několik způsobů počítání a postupně dojdeme k tomu správnému.

Tahle kapitola není zrovna čtení do tramvaje a může se stát, že nepochopíš všechno hned. Nic si z toho nedělej a po čase se k textu vrať. Když už budeš vědět, kudy, kam a proč směřuje, bude se ti číst a rozumět mnohem snáz. V každém případě je nutno nakonec vědět, jak se tedy množství informace počítá.

Na konci kapitoly využijeme matematickou funkci logaritmus. Pokud jste ji ještě neprobírali, příslušné pasáže přeskoč a vrať se k nim později.

Kolik otázek na kolik možností?

Úloha: Víc otázek, víc možností

Výška stromu

Drobné připomenutí: nejvyšší počet otázek potřebných k rozhodnutí podle daného stromu nazýváme také výška stromu. Pokud je strom optimální, odpovídá výška stromu optimálnímu počtu otázek.

Pokud postupujeme nejlépe jak to jde, odhalíme jednu z šestnácti možností pomocí čtyř otázek.
Z kolika nanejvýš možností si můžeme troufnout zjišťovat správnou, když budeme mít k dispozici 5 otázek?

1. 16/2=8; Každá další otázka sníží počet zbývajících možností na polovinu, možností bylo 16, z toho polovina je 8.
2. 16+1=17; Jedna otázka navíc nám umožní zjistit jednu možnost navíc.
3. (16/4)⋅5=20; Jednou otázkou umíme zjistit nanejvýš 16/4=4 možnosti, otázek máme pět, takže celkem 4*5=20 možností k zjišťování.
4. 5⋅5=25; Mezi šestnácti možnostmi se rozhodneme pomocí čtyř otázek, což je druhá odmocnina. Pro pět otázek tedy dostáváme 25 možností.
5. 16⋅2=32; Každá další otázka sníží počet zbývajících možností na polovinu, takže díky otázce navíc můžeme pracovat s dvojnásobkem možností.
6. Jiná možnost - jaká, proč?

Nápověda

• Nemusíš pracovat jen s představami, potřebné stromy si klidně nakresli.
• Zformuluj vlastní výsledek a vlastní zdůvodnění, to pak porovnej s nabídkou.
• Zkontroluj, jestli vybrané zdůvodnění funguje správně i pro jiné (menší) případy - jednu, dvě a tři otázky.
• Zkus si sestrojit příslušný optimální rozhodovací strom s pěti otázkami. Uvědom si, že není nutně potřeba doplňovat konkrétní otázky a možnosti. Už z pouhého tvaru stromu dokážeš spočítat, kolik je vespod možností odpovědí.

Řešení

E. 16⋅2=32; Každá další otázka sníží počet zbývajících možností na polovinu, takže díky otázce navíc můžeme pracovat s dvojnásobkem možností.

Úloha: Víc možností, víc otázek

Stejná situace z druhé strany: S kolika otázkami si troufneš hádat jednu možnost z 256 (to je 16²)?

1. 4+4=8; Čtyřmi otázkami určíme jeden ze 16 dílů o 256/16=16 možnostech, v tomto dílu najdeme správnou možnost opět pomocí 4 otázek.
2. √256=16; Když byly potřeba 4 otázky pro 16 možností, bude pro 16² možností potřeba 4² otázek.
3. 4⋅16=64; Když byly potřeba 4 otázky pro 16 možností, bude potřeba 16krát víc otázek pro 16krát víc možností.
4. 256/2=128; Každá otázka ubere polovinu možností, polovina z 256 je 128.
5. 4+(256-16)=244; Když byly potřeba 4 otázky pro 16 možností, bude pro dalších 240 možností potřeba dalších 240 otázek.
6. 256-1=255; Strom pro 16 možností obsahuje 15 otázek, strom pro 256 možností bude obsahovat 255 otázek.
7. Jiná možnost - jaká, proč?

Nápověda

Použij obdobu postupů z předchozí otázky. Navíc můžeš použít i zjištěnou odpověď.

Řešení

A. 4+4=8; Šestnáct možností je třeba rozpůlit čtyřikrát, 256 možností je třeba navíc půlit ještě čtyřikrát.

Úloha: Jaký je vztah mezi počtem potřebných otázek a počtem rozlišitelných možností?

Vytvoř v tabulkovém procesoru pomůcku na určování počtu rozlišitelných možností podle počtu otázek. Např. v jednom sloupci může postupně narůstat počet otázek, ve vedlejším sloupci se vypočítá (nebudeš to přece vyplňovat ručně...) příslušný počet možností.

Zkratka

Vztah mezi počtem možností a počtem potřebných otázek umíme popsat jako počet postupných vydělení počtu možností dvěma. Znáš matematickou funkci, která právě tohle vyjadřuje?

Kdo poctivě sestrojoval stromy, bezpečně odhalil, jak přijít od počtu otázek k počtu možností a naopak. Jedna otázka rozliší dvě možnosti. Se dvěma otázkami už rozlišíme čtyři možnosti. Každá otázka navíc znamená jedno rozpůlení možností navíc, a umožňuje tak začít s dvojnásobkem možností. Máme-li k dispozici n otázek, můžeme při optimálním postupu rozlišit nanejvýš 2ⁿ možností.

Pamatuj si:

#V informatice někdy při počítání značíme "počet" znakem "#", anglicky někdy "number sign". Značka se ale hodí třeba i při psaní poznámek z výuky.možností = 2^#otázek

Chceme-li naopak zjistit počet potřebných otázek k uhodnutí čísla z daného rozsahu, můžeme spočítat, kolikrát rozsah (počet možností) vydělíme dvěma, než se dobereme k jediné zbývající možnosti.

Úloha: Jak počítat potřebný počet otázek, když máme možností lichý počet?

Zajímá nás, kolik otázek k uhodnutí stačí jistě — tedy i v případě, že se nám vůbec nedaří. Pro příklad uvažujme 23 možností. Kolik je potřeba otázek k uhodnutí jednoho čísla z 23 možných?

Nápověda

Můžeme mít smůlu, a vyloučit "menší polovinu" možnosti. Pro další půlení proto musíme vždy počítat s tou "větší polovinou".

Řešení

Při 23 možnostech bude půlení postupovat takto:

• 23=11+12
• 12=6+6
• 6=3+3
• 3=1+2
• 2=1+1

Možnosti jsme půlili pětkrát, potřebujeme tedy 5 otázek.

Když budem mít štěstí, může se počet možností snižovat takto: 23 → 11 → 5 → 2 → 1. V takovém případě by tedy stačily čtyři otázky. Na štěstí se ale spoléhat nechceme, proto budeme raději počítat s otázkou navíc.

Jak může pro různé počty možností vyjít stejný počet otázek?

23 možností vyžaduje 5 otázek, stejně jako 32 možností (a stejně jako libovolný jiný počet v rozsahu 17-32). Někomu možná připadá zvláštní, že různý počet možností vyžaduje stejný počet otázek. Vyplývá to ze struktury rozhodovacího stromu. Zamyslete se: Připadá někomu z vás zvláštní, že máte dva rodiče, čtyři prarodiče, osm praprarodičů atd.? Není žádná generace, ve které byste měli třeba 6 nebo 7 přímých předků.

Tušení, že se možnosti „navíc“ musí někde projevit (i když nejvyšší počet potřebných otázek se neliší), je ale správné. Rozdíl se projeví v počtu potřebných otázek při opakovaném hraní.

Jiné vyjádření

Kromě „s jednou otázkou navíc rozeznáme dvojnásobek možnosti“ můžeme říct také „s dvojnásobkem otázek rozeznáme druhou mocninu původního počtu možností“.

Všimni si toho nepoměru: přidání jediné otázky umožní zdvojnásobit počet zjistitelných možností. Na 16 možností jsou potřeba 4 otázky, na 32 je třeba 5 otázek. Na 1000 možností stačí 10 otázek, na milion možností stačí 20 otázek. Přitom naivní tipování by otázek vyžadovalo v průměru půl milionu, a s trochou smůly skoro celý milion! Tak jako leckde jinde, i v informatice se chytré postupy nejlépe projeví ve velkých měřítkách.

Vztah výšky optimálního stromu k počtu listů. Je ti tvar toho grafu povědomý?

Množství informace, počet vyloučených možností a nezávislé zprávy

Množství informace závisí na příjemci

Množství informace ve zprávě není jen vlastnost té zprávy. Je to vlastnost zprávy spolu s příjemcem (stavem jeho znalosti). Když tedy dva různí příjemci uvažují s různými možnostmi (každý ví o skutečnosti něco trochu jiného), může pro ně být informační hodnota stejné zprávy velmi rozdílná. Pokud vím, že je po poledni, neřekne mi už zpráva „Je po Večerníčku“ tolik, jako mému kamarádovi, který to neví.

Podobně se mění množství informace v téže zprávě přijaté opakovaně stejným příjemcem. Prvním přijetím zprávy se něco nového dozví, množství získané informace je kladné. Když ovšem zprávu přijímá znovu, nic nového se v ní nedozví (její obsah už zná z dřívějška), takže je množství přijaté informace nulové.

Už toho o informacích víme poměrně hodně: co jsou zač, jak je efektivně získávat, a jak dlouho to kdy trvá. Jak tedy poměřujeme, která zpráva přináší více informace? Lze množství informace nějak vyčíslit? Kolik jsme se toho dozvěděli přijetím zprávy, můžeme posoudit jako rozdíl mezi tím, kolik jsme toho nevěděli před přijetím zprávy, a tím, kolik toho nevíme po jejím přijetí. Budeme tedy hledat vzoreček ve tvaru:

Pamatuj si:

„množství informace“ = „neurčitost před zprávou“ — „neurčitost po zprávě“

Přitom míra neurčitosti závisí na počtu zbývajících možností: čím je jich víc, tím méně víme.

Úloha: Nemám tušení, kolik je hodin

Šel jsem spát neskutečně unavený, spal jsem neurčitě dlouho a probral se v místnosti bez hodin, oken či jiného způsobu, jak určit denní dobu. Zajímá mne čas s přesností na minuty.

Otázka: Kolik je možností pro denní dobu s přesností na minuty?

Nápověda

Otázka vlastně zní: kolik různých denních dob existuje? Nenapadne-li tě nic lepšího, budeš si je muset všechny vypsat. V průběhu třeba objevíš, jak si při tom ušetřit práci a dojít k výsledku rychleji.

Řešení

Den má 24 hodin, každá z nich má 60 minut. 24⋅60 = 1440.

Otázka: Kolik dobrých otázekTakových, co vedou k výsledku nejkratší cestou. se dvěma možnými odpověďmi jistě stačí k určení denní doby s přesností na minuty?

Nápověda

Použij stejný princip jako u čísel a zvířat. Kolikrát je třeba zbývající možnosti omezit na polovinu, než zbyde jediná poslední?

Řešení

Postupně dělíme 1440 možností na poloviny a zapisujeme si mezivýsledky. V případě lichého počtu možností zaokrouhlujeme nahoru.
Mezivýsledky: 1440, 720, 360, 180, 90, 45, 23, 12, 6, 3, 2, 1
Celkem jsme uskutečnili 11 dělení, k určení denní doby je tedy potřeba položit nanejvýš 11 dobrých otázek.

Možnost dalšího procvičení

Kolik možností uberou jednotlivé dvojice zpráv? Kolik větší skupinky?
Například dvojice „Je po poledni“ a „Je sudá hodina“ uberou celkem 1080 možností a ponechají jich 360.

Uvažujme následující zprávy:

1. Je po poledni.
2. V místní škole ještě probíhá výuka.
3. Je tři čtvrti na (nějakou) celou.
4. Je sudá hodina.
5. Je před Večerníčkem.
6. Je víc minut než hodin.
7. Je mezi půl desátou dopoledne a půl šestou večer.
8. Je tři čtvrti na tři.

A

B

C

D

E

F

G

H

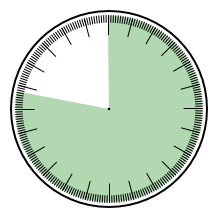
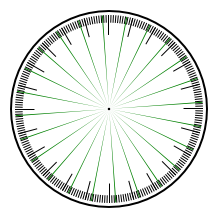
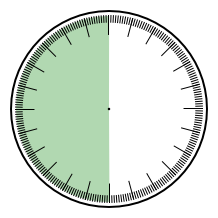
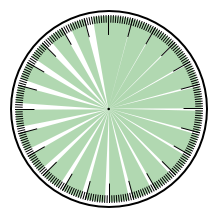
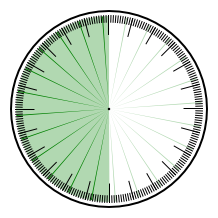
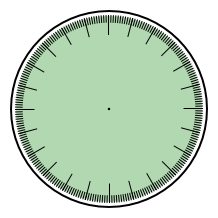
Otázka: Které zprávě odpovídá který obrázek? Ciferníky jsou 24hodinové, zelená označuje možnou denní dobu podle dané zprávy.

Řešení

1F, 2A, 3E, 4H, 5D, 6G, 7B, 8C.

Otázka: Kolik možností uberou jednotlivé výše uvedené zprávy?

Nápověda

Ubrané možnosti odpovídají bílé ploše na cifernících. Někdy je snazší spočítat, kolik možností zbyde. U zprávy B (doba výuky) odpověď odhadni podle místních podmínek. K počítání se hodí kalkulátor, třeba tabulkový.

Řešení

Např. zpráva Je tři čtvrti na (nějakou) celou omezuje možnou denní dobu na 24 možností, všechny ostatní tedy ubrala. 1440-24=1416 ubraných možností. Zpráva Je mezi půl desátou dopoledne a půl šestou večer zahrnuje 8 hodin, vylučuje jich tedy 16. Každá hodina představuje 60 možností (zajímáme se o čas s přesností na minuty), 16⋅60=960 ubraných možností.

Ciferník se zprávou	Po poledni.	Probíhá výuka.	Tři čtvrti.	Sudá hodina.	Před Večerníčkem.	Víc minut než hodin.	9:30-17:30.	14:45
Počet vyloučených možností	720	990Uvažovali jsme výuku od 8 do 15:30.	1416	720	315Večerníček začíná v 18:45	300Není 0:00, 1:00, 1:01, 2:00, 2:01, 2:02, ..., 23:22, 23:23. Ubylo tedy 1+2+3+...+23+24 možností.	960	1439

 

Otázka: Jaký podíl zbývajících možností uberou jednotlivé výše uvedené zprávy?

Nápověda

Nezapomeň využít předchozí výsledky. K počítání se hodí kalkulátor, třeba tabulkový.

Řešení

Ciferník se zprávou	Po poledni.	Probíhá výuka.	Tři čtvrti.	Sudá hodina.	Před Večerníčkem.	Víc minut než hodin.	9:30-17:30.	14:45
Počet vyloučených možností	720	990Uvažovali jsme výuku od 8 do 15:30.	1416	720	315Večerníček začíná v 18:45	300Není 0:00, 1:00, 1:01, 2:00, 2:01, 2:02, ..., 23:22, 23:23. Ubylo tedy 1+2+3+...+23+24 možností.	960	1439
Podíl vyloučených možností	1/2	99/144=0,6875	59/60≈0,9833	1/2	315/1440≈0,2188	300/1440≈0,2083	2/3	1439/1440≈0,9993

 

Jak tedy měřit množství informace? Mohli bychom zkusit použít přímo počty vyloučených možností. Zpráva „Je tři čtvrti na celou“ by tak nesla 1416 „jednotek informace“Protože den má 24*60=1440 minut a zpráva vyloučila všechny kromě 24, které jsou právě „ve tři čtvrti“: 1440-24=1416. Rychle se ale ukáže, že takový postup nefunguje dobře.

Příklad: Nezávislé zprávy

Odpolední výuka: Probíhá výuka a zároveň je po poledni.

Je po poledni a zároveň je tři čtvrti na celou.

Uvažujme zprávy „Je po poledni“ a „Je tři čtvrti na celou.“ Ty dvě zprávy na sobě nejsou nijak závislé: Z toho, že je po poledni, se nedozvím vůbec nic o tom, jestli je tři čtvrtě, a naopak. Nic na tom nemění, že i po poledni nastane několikrát okamžik „tři čtvrtě“ (ani že několik z možných „tři čtvrtě“ se odehraje po poledni).

Závislé jsou naopak zprávy „Je po poledni“ a „V místní škole ještě probíhá výuka.“ Z jedné můžeme aspoň přibližně usuzovat o platnosti druhé. Probíhá-li vyučování, je pravděpodobně spíš dopoledne, než odpoledne, protože dopoledne probíhá větší část vyučování. A naopak, je-li po poledni, ještě silněji než před tímto zjištěním teď předpokládáme, že vyučování spíš neprobíhá.

Uvažujme nezávislé zprávy z příkladu a měření informace počtem vyloučených možností. „Je po poledni“ by neslo 720 nějakých jednotek informace, '„Je tři čtvrti na celou“ by jich neslo 1416. Nebo ne? Pokud už víme, že je po poledni, vyloučí zpráva „Je tři čtvrti na celou.“ nikoliv 1416, ale už jen 708 možností. Takže by najednou nesla jen 708 jednotek informace. To je ale problém. Nechceme přece, aby se množství informace ve zprávě měnilo s tím, jak se dozvídáme něco s tou zprávou nesouvisejícího.

Požadované vlastnosti měřítka na informace

Měření informace tedy patrně musí splňovat některé požadavky, aby výsledky dávaly dobrý smysl a odpovídaly našim přirozeným představám. Mezi takové požadavky patří především:

Zpráva o přesném čase (14:45) poskytne všechnu chybějící informaci a odstraní veškerou neurčitost.

Tato zpráva vyloučí víc možností, poskytne proto víc informace.

Stejný počet možností vyloučí zpráva „Je po poledni“.

Zpráva „Je sudá hodina“ vyloučí právě polovinu možností (bílá plocha).

Dolní mez

Množství informace, jako každé jiné množství, musí být nezáporné. Ve zprávě, která neubere žádné možnosti, je množství informace nulové.

Horní mez

Toho dosáhne taková zpráva, ze které se dozvíme vše, neboli zbyde jediná možnost.

Úměra

Čím více možností zpráva ubere, tím více obsahuje informace (úměra ale nemusí být přímá!).

Vyplývající zprávy

Jestliže z jedné zprávy (např. „Je to savec.“) přímo vyplývá zpráva druhá (např. „Je to obratlovec“), je v první zprávě přinejmenším tolik informace, kolik je v té druhé.

Nezávislé zprávy

Informační hodnota nezávislých zprávJedna z druhé ani částečně nevyplývá, např. „Je po poledni“ a „Je tři čtvrti na celou.“ nezáleží na pořadí jejich získání. Navíc když získáme obě zprávy, množství celkově získané informace je přesně rovno součtu množství informace v obou zprávách.

Kvantita, nikoliv kvalita

Množství informace záleží pouze na počtech možností, nikoliv na tom, které konkrétní možnosti ubyly. Zpráva „Je po poledni“ nese stejné množství informace jako zpráva „Je sudá hodina.“
Podobně se množství informace nemá měnit se změnou komunikačního kanálu. Musí být jedno, jestli informaci získáme z videa na YouTube nebo z mezopotámské hliněné destičky.

Další požadavky

Převoditelnost

My pro jednoduchost připouštíme jen dvě možné odpovědi na otázku. V principu ale můžeme pracovat i s otázkami bohatšími. Naměřené množství informace v různých situacích přitom musí být buď stejné, nebo vzájemně jednoznačně převoditelné (podobně jako např. rychlost větru v m/s na km/h či imperiální na metrické jednotky).

Závislé zprávy

Pokud obsahy dvou zpráv souvisíPřijetím jedné zprávy se pro nás změní množství informace ve druhé zprávě., mělo by platit: Celkové množství informace získané oběma zprávami je rovno součtu množství informace v obou zprávách zmenšenému o množství informace, které obě zprávy sdílí. Jinými slovy odečteme to, co bychom jinak započetli dvakrát. Obdobně počítáme velikost sjednocení množin s neprázdným průnikem.

Uvedené vlastnosti jsou poměrně přirozené, proč je tedy tak podrobně probíráme? Protože díky jejich přesnému určení snáze odhalíme jediný možný způsob, jak množství informace měřit. Podívejme se na dvě nezávislé zprávy, např. „Je tři čtvrti na celou“ a „Je sudá hodina.“

Jak změřit, kolik toho nevíme?

Měření informace bez logaritmu

Zde uvedený výklad se pokud možno vyhýbá pojmu logaritmu. Je to proto, že se s ním studenti leckde seznamují poměrně pozdě, a ani potom mu dobře nerozumí.

Pokud jsou pro ně ovšem následující vztahy přirozené, nebo aspoň srozumitelné, lze měření množství informace vyložit přímočařeji a dostat se při tom hlouběji:

• Logaritmus je inverzní k exponenciální funkci. Odpovídá na otázku „na kolikátou mám umocnit základ, abych dostal daný výsledek?“
• Výška optimálního rozhodovacího stromu je vzhledem k počtu listů logaritmická (o základu 2). Např. 8 prarodičů máme o log(8)=3 generace zpět.
• Logaritmus převádí násobení na sčítání, pravidlo log(a⋅b)=log(a)+log(b) není jen nahodilost určená k úpravám výrazů.

Pokud si naopak vystačíme i se vzájemným porovnáváním množství informace ve zprávách a nebudeme jej chtít vyčíslit, obejdeme se bez logaritmu úplně.

Úloha: Doplň tabulku

Následující tabulka zachycuje čtyři situace postupného přijímání zpráv „Je tři čtvrti na celou“ a „Je sudá hodina“: Buď na začátku nevíme nic, a obdržíme jednu ze zpráv, nebo už jednu ze zpráv máme, a obdržíme tu druhou. Otázkou je, kolik možností se ve kterém případě vyloučí, což by mělo nějak souviset s množstvím informace v jednotlivých zprávách. To by se navíc nemělo nijak změnit podle toho, jestli už máme druhou zprávu, protože jsou obě zprávy nezávislé.
Doplň chybějící hodnoty.

Co vím předem	Možnosti předtímPočet možností před přijetím zprávy	Otázky předtímKolik otázek (resp. odpovědí ANO nebo NE) potřebuji k určení správné možnosti z daného počtu		Co se dozvímJakou zprávu dostávám: „Je tři čtvrti na celou“ nebo „Je sudá hodina.“	Možnosti potomPočet možností zbylých po přijetí zprávy	Otázky potomPočet otázek (resp. odpovědí ANO nebo NE) nutných k vyloučení možností zbylých po přijetí zprávy		Vyloučené možnostiPočet možností, které jsme mohli vyloučit po přijetí zprávy	Podíl vyloučených možnostíPodíl počtu vyloučených a původních možností	Úbytek otázekPočet otázek, které díky zprávě nebudeme muset položit
nic	1440	11		Tři čtvrti	24				1416/1440 = 59/60
Sudá hodina		10
nic	1440			Sudá hodina	720			720
Tři čtvrti						4		12		1

Řešení

Co vím předem	Možnosti předtímPočet možností před přijetím zprávy	Otázky předtímKolik otázek (resp. odpovědí ANO nebo NE) potřebuji k určení správné možnosti z daného počtu		Co se dozvímJakou zprávu dostávám: „Je tři čtvrti na celou“ nebo „Je sudá hodina.“	Možnosti potomPočet možností zbylých po přijetí zprávy	Otázky potomPočet otázek (resp. odpovědí ANO nebo NE) nutných k vyloučení možností zbylých po přijetí zprávy		Vyloučené možnostiPočet možností, které jsme mohli vyloučit po přijetí zprávy	Podíl vyloučených možnostíPodíl počtu vyloučených a původních možností	Úbytek otázekPočet otázek, které díky zprávě nebudeme muset položit
nic	1440	11		Tři čtvrti	24	5		1416	1416/1440 = 59/60	6
Sudá hodina	720	10			12	4		708	708/720 = 59/60	6
nic	1440	11		Sudá hodina	720	10		720	720/1440 = 1/2	1
Tři čtvrti	24	5			12	4		12	12/24 = 1/2	1

Znovu vidíme, že počet vyloučených možností k vyjádření množství informace ve zprávě použít nelze. Liší se totiž podle toho, co už víme z jiné, nezávislé zprávy. Co se tedy v tabulce pro jednotlivé zprávy nemění?

Samostatný průzkum

Máme-li čas a šikovné studenty, můžeme samozřejmě nechat i tuto slepou (byť nápomocnou) uličku prozkoumat samotné studenty.

Poměr vyloučených a původních možností

Zpráva	„Je sudá hodina.“	„Je tři čtvrti na celou.“	„Je tři čtvrti na nějakou lichou hodinu.“	„Je tři čtvrti na tři.“
Jak by vypadalo měření „množství informace“ pomocí poměru vyloučených možností	1/2 = 0,5	59/60 ≈ 0,983	1/2+59/60 = 89/60 ≈ 1,483 To je víc než 1!	1439/1440 ≈ 0,999

Poměr vyloučených a původních možností se nemění. Bude tedy pro nás patrně užitečnější, než samotný konkrétní počet možností. To odpovídá i naší snaze při hádání myšleného čísla. Informace se chceme dozvídat plynule, ne tak, aby se ke konci dotazování zmenšoval informační přínos jednotlivých odpovědí s tím, jak ubývají možnosti. A každou otázkou se snažíme ubrat polovinu možností, tedy nikoliv konkrétní počet, nýbrž konkrétní podíl možností.

Nemůžeme ale říct, že by zpráva „Je sudá hodina.“ obsahovala 1/2 jednotky informace a zpráva „Je tři čtvrti na celou“ potom 59/60 jednotky informace. Sečtení množství informace obsažené v obou zprávách (což odpovídá zprávě „Je tři čtvrti na nějakou lichou hodinu“) by dávalo 89/60 jednotky informace. To je ovšem nesmysl, protože to je víc, než případných 1439/1440 jednotky informace, které už plně určují denní dobu! Čistě pomocí podílu vyloučených možností tedy informace měřit nepůjde, musíme hledat dál.

Rozdíl v počtu potřebných otázek

Kromě podílu se v tabulce nemění také rozdíl v počtu otázek potřebných k určení přesného času před a po přijetí zprávy. Můžeme tedy pro měření informace použít právě tento rozdíl?

Příklad: Měření množství informace prostřednictvím rozdílu v počtu potřebných otázek

Měření množství informace počtem ušetřených otázek

Zpráva	„Je sudá hodina.“	„Je tři čtvrti na celou.“	„Je tři čtvrti na nějakou lichou hodinu.“	„Je tři čtvrti na tři.“
Otázky předtímPočet otázek (resp. odpovědí) ANO nebo NE nutných k vyloučení počátečních možností	11	11	11	11
Otázky potomPočet otázek (resp. odpovědí) ANO nebo NE nutných k vyloučení možností zbylých po přijetí zprávy	10	5	4	0
Množství informace (ušetřené otázkyPočet otázek, které díky zprávě nebudeme muset položit.)	11-10 = 1	11-5 = 6	11-4 = 7	11-0 = 11

Z předchozích výpočtů už víme následující:

Na začátku jsme o přesném čase věděli tak málo, že bychom k jeho určení potřebovali položit 11 otázek. Po přijetí zpráv „Je sudá hodina.“ a „Je tři čtvrti na celou.“ bychom se potřebovali doptat na 4 otázky. To odpovídá celkovému úbytku 1+6 = 7 otázek prostřednictvím těch dvou zpráv. Sčítání množství informace v nezávislých zprávách zde tedy funguje.

Měření neurčitosti počtem potřebných otázek tedy splňuje naše podmínky. Navíc dává dobrý smysl: Množství informace ve zprávě odpovídá počtu otázek, které díky zprávě při vylučování možností ušetříme (nebudeme je muset položit). Jinými slovy, pokud chceme příslušný údaj zjistit pokládáním otázek, musíme jich položit právě tolik, kolik je ve zprávě informace.

Pamatuj si:

„množství informace“ ≈ „otázky předtím“Počet otázek nutných k vyloučení počátečních možností - „otázky potom“Počet otázek nutných k vyloučení možností zbylých po přijetí zprávy

Pozorný čtenář si všiml, že v zelenomodré tabulce pracujeme s počtem otázek, který jistě stačí k určení času při daných znalostech. Protože ale zbývající možnosti nejsou mocninou čísla 2, bude někdy stačit otázek méně. Naše výpočty jsou tedy zatím pouze přibližné.

Základní jednotka informace

Už víme, jak informaci měřit, ale neřekli jsme si, v jakých jednotkách. Je to ale nasnadě: V počtu odpovědí na otázky. Přitom máme na mysli otázky, které umožňují právě dvě odpovědi. Z hlediska množství informace je jedno, jestli jsou to odpovědi ano a ne, < a ≥, pravda a nepravda, sluníčko a obláček, zapnuto a vypnuto či číslice 1 a 0. Právě ty číslice jsou ale poměrně praktické. Jsou krátké, a lze je podle potřeby používat jako logické hodnoty (pravda a nepravda, technicky potom zapnuto a vypnuto) nebo jako čísla, reprezentující cokoliv, co jsme naměřili nebo očíslovali. Příslušnou jednotku informace už jistě znáš z dřívějška.

Pamatuj si:

Základní jednotkou informace je bit, z anglického binary digit. Značíme ji malým tiskacím písmenem b. Bit je jedna dvojková číslice, představuje tedy rozhodnutí mezi dvěma možnostmi(nebo skupinami jednotlivých možností). Jeden bit informace vyloučí právě polovinu zbylých možností. (Dva bity(tedy dvě číslice, nebo také dvě odpovědi (ano nebo ne) vyloučí polovinu možností a ze zbytku opět polovinu, takže z původních možností zbyde čtvrtina.)

O bitech se hovoří také v souvislostí s pamětí počítače: bit je místo pro uchování jedné číslice 0 nebo 1, tedy bitu. Je to podobná zkratka, jako když řekneš, že lahev má litr, když chceš říct, že je v ní prázdné místo pro litr nějaké tekutiny. Není to úplně přesné, ale souvislost je jasná a porozumění to nijak nebrání.

Přesné měření

Někteří si možná během úloh ušetřili spoustu práce. Uvědomili si, že počet potřebných otázek (neboli výšku optimálního stromu) nemusí zjišťovat ručně jako počet postupných dělení dvěma. To za nás přece dovede spočítat funkce logaritmus!

Úloha:

Pokud jsi to ještě nezkusil(a), přesvědč se o tom. Vyřeš některou z předchozích úloh s pomocí dvojkového logaritmu.

Nápověda

Zejména ti, kdo v matematice ještě logaritmy neprobírali: podívejte se do přípravné kapitoly -tady bude odkaz-.

Řešení

Např. jsme řešili, kolik otázek je třeba k určení denní doby, tedy jedné z 24*60=1440 možností. Stačí spočítat dvojkový logaritmus:

log(1440) ≈ 10,49

Těžko položíme 0,49 otázky, potřebujeme tedy 11 otázek. Logaritmus nám ušetřil nutnost postupného dělení dvěma.

Při použití logaritmu v informatice je třeba dávat pozor na použitý základ. Např. na kalkulačkách obvykle najdeme přirozený a dekadický logaritmus, ale nikoliv dvojkový. To dává smysl, většina lidí nejsou informatici. Nezapomeňte tedy výsledky převést na logaritmus o správném základu.

Základ 2 používáme právě proto, že pracujeme se dvěma hodnotami. Výsledky tak přirozeně vycházejí v bitech. Logaritmus je v informatice dvojkový tak často, že už jej všichni předpokládají a není třeba jej uvádět (pozn.Pokud ale používáme logaritmus mimo informatiku, je třeba se buď ujistit, že se na základu všichni shodují, nebo ho jasně uvést.). Logaritmus nám navíc dá smysluplné výsledky i v případě, že počet možností není celočíselnou mocninou dvou, takže musíme pracovat s přibližnou hodnotou.

Příklad: Informace ve zprávě „Je tři čtvrti na celou“

„Je tři čtvrti na celou.“

Zpráva redukuje možnosti na 1/60 původního počtu. Tohle množství v celých bitech vyjádřit nelze. Pomocí šestibitové zprávy(tedy pomocí šesti půlení) bychom totiž totiž měli být schopni zredukovat možnosti na 1/64 původního počtu, a ne jenom na 1/60. Přitom 5 bitů(pět půlení) je málo, pětibitová zpráva zredukuje možnosti jen na 1/32. Skutečné množství informace tedy musí být někde mezi tím, mezi 5 a 6 bity (a zřejmě blíž k 6). Dvojkový logaritmus nám dá přesný výsledek.

Vyjdeme ze vztahu uvedeného výše, množství informace je rozdíl mezi počtem otázek potřebných před a otázek potřebných po přijetí zprávy. Místo počítání otázek postupným dělením použijeme logaritmus. Na začátku máme 1440 možností, po přijetí zprávy už jen 24:

log(1440) - log(24) ≈ 10,49 - 4,58 ≈ 5,91 b

Zpráva „Je tři čtvrti na celou“Samozřejmě jen v dané situaci, tedy když nás zajímá denní doba s přesností na minuty a před přijetím zprávy netušíme nic. tedy nese přibližněMůžeme použít libovolnou přesnost, se kterou dovedeme počítat logaritmy. 5,91 bitů informace.

A co sčítání množství informace v nezávislých zprávách?

Logaritmus pro leckoho není zrovna intuitivní funkce. Máme jistotu, že bude vše správně fungovat i pro kombinování nezávislých zpráv? Opravdu se množství informace získané přijetím dvou nezávislých zpráv rovná součtu množství informace v jednotlivých zprávách i v případě, že počítáme pomocí logaritmu?

Využijeme toho, že množství informace ve zprávě je rovno logaritmu z poměru počtu možností před a po přijetí zprávy. Jsou-li zprávy a a b nezávislé, poměry počtů možností P_a a P_b zůstávají zachovány nezávisle na přijetí či nepřijetí druhé zprávy. Pokud přijmeme obě zprávy (v libovolném pořadí), je celkový poměr počtu možností před a po přijetí obou zpráv roven součinu dílčích poměrů P_a⋅P_b (to si promysli!).

Chceme tedy ověřit, jestli platí, že celková získaná informace je součtem informací z dvou nezávislých zpráv:

log(P_a⋅P_b) = log(P_a)+log(P_b)

Když se ale na vztah trochu pečlivě zadíváme, zjistíme, že není co ověřovat. Už víme, že platí, je to totiž základní vlastnost logaritmu. Vidíme tedy, že sčítání a logaritmy společně dávají smysluplné výsledky. Informatici na logaritmy nedají dopustit.

Příklad: Množství informace ještě úsporněji

Nakonec na stejném příkladu ukažme, jak ušetřit práce ještě víc. Opět uvažujeme zprávu „Je tři čtvrti na celou.“, 1440 počátečních možností a 24 možností koncových. Tentokrát si ale navíc vzpomeneme na užitečnou vlastnost logaritmů:

log(a⋅b) = log(a)+log(b), neboli log(a)-log(b) = log(a/b)

Dostaneme tak:

log(1440) - log(24) = log(1440/24) = log(60) ≈ 5,91 b

Logaritmus tedy stačí počítat jen jeden. Všimni si navíc poměru 1440/24=60. Tedy před přijetím zprávy jsme měli 60krát víc možností, než po něm. Pokud u zprávy známe tento poměr, není třeba jednotlivé možnosti počítat vůbec!

Pamatuj si:

Množství informace ve zprávě je rovno logaritmu z poměru počtu možností před a po přijetí zprávy.

Po dlouhé cestě jsme se dopracovali k překvapivě jednoduchému vztahu. Ovšem jen díky tvému vlastnímu vytrvalému úsilí víš, co se za vzorečkem skrývá a jak se k němu dojde.

Shrnutí

Máme-li k dispozici n otázek, můžeme při optimálním postupu rozlišit nanejvýš 2ⁿ možností.

Množství informace odvozujeme od rozdílu v tom, co jsme věděli před jejím přijetím, a co víme po jejím přijetí.

Základní jednotkou informace je bit (značený b), neboli binárnídvojková číslice. Jeden bit informace vyloučí právě polovinu zbývajících možností. Množství informace v bitech odpovídá počtu otázekOptimálních (půlících) otázek s odpovědí ANO nebo NE., které díky dané informaci nebudeme muset položit.

Množství informace ve zprávě je rovno logaritmu z poměru počtu možností před a po přijetí zprávy.