Vývojové diagramy
Co se naučíš:
- Vědět, k čemu je vývojový diagram dobrý a v odpovídající situaci ho použít.
- Číst hotový vývojový diagram a pracovat podle něj.
- Vytvořit či upravit vývojový diagram.
Přirozený jazyk mnohdy není ideálním nástrojem pro popis pracovního postupu. Jeho interpretace je obtížná a jazyk sám často umožňuje nepřesné vyjadřování. To je v životě mnohdy praktické, ale pro algoritmy se to vůbec nehodí. Podíváme se proto na dva jiné způsoby popisu pracovního postupu: vývojové diagramy a potom na programování.
S vývojovými diagramy se běžně setkáš kdykoliv, kdy je třeba popsat postup, ve kterém bychom se při ručním provádění snadno ztratili.
Jednoduchým příkladem vývojového diagramu může být rozhodovací strom.
Rozhodovací strom je zjednodušeným případem vývojového diagramu. Princip ale zůstává stejný: Plníme instrukce v jednotlivých blocích a postupujeme po spojovacích čarách, dokud nedojdeme do konce. V rozhodovacím stromu jsme začali nahoře a bloky vždy obsahovaly otázku, na základě které jsme se rozhodli o dalším postupu. Vývojový diagram je o něco bohatší.
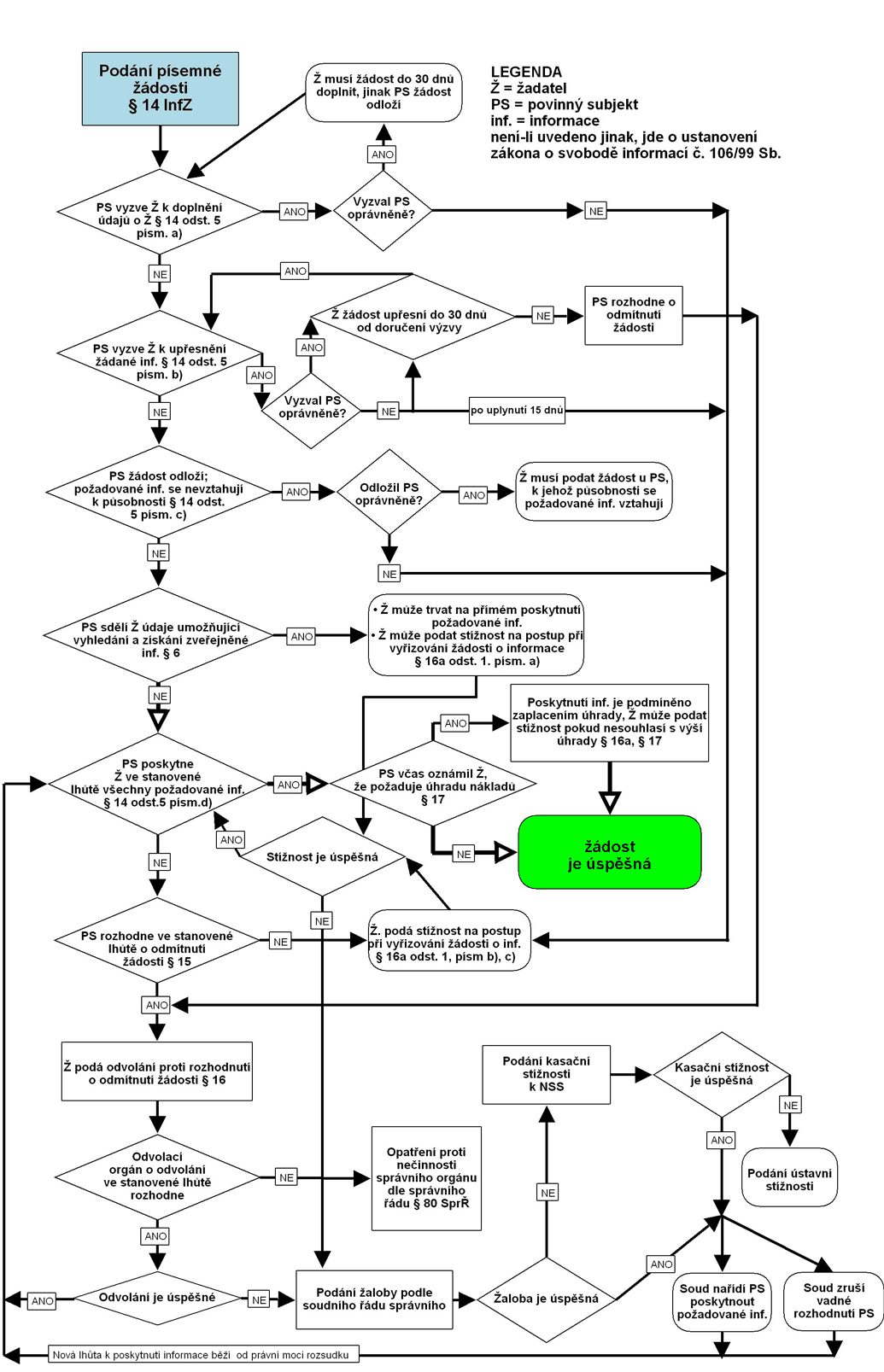
Tento diagram ukazuje už dříve uvedený postup přípravy míchaných vajec. Srovnej oba popisy — dělají totéž? Vidíme nové tvary bloků, které nám usnadní čtení vývojových diagramů a tím pádem i porozumění samotným algoritmům.
- Začátek a konec jsou označeny obdélníkem se zaoblenými rohy.
- Do obdélníku píšeme příkazy neboli instrukce.
- Kosodélník označuje příkazy vstupu a výstupu, tedy místa, kde postup přijímá či vydává informace nebo jiný materiál.
- V kosočtverci jsou podmínky k rozhodnutí, kudy pokračovat. Rozhodovací podmínky znáš z tabulkového procesoru v souvislosti s funkcí [KDYŽ (případně IF).
Vývojové diagramy musí splňovat zásady, které asi očekáváš, např.:
Studenti by měli pochopit, že smyslem přiměřeně správného použití tvarů bloků v diagramech není tyranie učitele, ale nástroj k jejich lepší přehlednosti a tím i použitelnosti.
- Začátek je v diagramu vždy právě jeden.
- Z každého bloku (kromě rozhodovacího) vede jen jediná spojnice, aby bylo jasné, kudy pokračovat.
- Spojnice vedoucí z rozhodovacího bloku musí být označeny (typicky ano-ne, pravda-nepravda, P-N, true-false, T-F, 1-0…), aby bylo jasné, kterou vybrat v jakém případě.
- Spojnice nesmí začínat či končit „ve vzduchu“. Vždy vede z bloku do bloku, nebo se připojí na jinou spojnici.
- U každé spojnice musí být jasný směr postupu.
Tato (a další podobná) pravidla usnadňují dodržení vlastností algoritmů, především jednoznačnosti postupu.
Spojnice ve vývojovém diagramu mohou (na rozdíl od spojnic rozhodovacího stromu) vést i zpět na místa, kde už jsme byli. To nám dává možnost několikrát zopakovat stejné kroky, např. pravidelně míchat vejce, dokud nejsou hotová. Takové konstrukci říkáme cyklus. Je samozřejmě potřeba dát pozor na to, aby cyklus někdy skončil. Pokud se postup tzv. zacyklí, nikdy neskončí a není to algoritmus.
Vyber si některý diagram z této stránky, najdi jeho nedostatky a uveď, jak ty nedostatky brání snadnému provedení postupu podle diagramu. Zkus daný diagram samostatně vylepšit (především co do formy, ale třeba tě napadne i obsahové vylepšení).
Řešení
Mezi typické chyby patří nerozlišování tvarů bloků, chybějící šipky a křížení čar, označení odpovědí „ano“ a „ne“ někde daleko od otázky (nejasný směr postupu), neoznačený začátek a konec…
I přes všechny tyto chyby jsou ovšem vývojové diagramy přehlednější, než textové popisy!
Postupy podle vývojového diagramu provádí zpravidla člověk, nikoliv počítač. Pravidla proto nejsou dodržována zcela striktně (i když technické normy pro vývojové diagramy existují). Především samotný obsah bloků závisí na oblasti použití postupu. Někde můžeme použít matematické zápisy, někde zdrojový kód jako v programování, někde ale musíme použít přirozený jazyk. Vývojové diagramy tedy pomáhají zajišťovat přehlednost a jednoznačnost postupu, ovšem elementárnost, konečnost a další podobné otázky musí ohlídat autor.
Analýza existujícího diagramu
Příklad: Záhadný diagram
Podívej se na následující vývojový diagram.
Rozlišovat přiřazení a porovnání v samotných vývojových diagramech by nebylo zcela nutné. Zmatek by ovšem nastal při pokusu něco skutečně naprogramovat. Proto pokládáme za lepší pro pořádek obě možnosti rozlišovat rovnou.
V informatice rozlišujeme různé významy „rovná se“. To dvojité (==) v podmínce (v kosočtverci) znamená porovnání, lze ho číst jako „Hodnota proměnné x je rovna hodnotě proměnné y.“ Z rozhodovacího bloku pokračujeme podle toho, jestli podmínka platí, nebo neplatí. Samo o sobě dvojité rovnítko nic nedělá.
Jednoduché rovnítko v příkazech dole znamená přiřazení. Čteme jej tedy např. jako „Do proměnné y přiřaď rozdíl y-x.“ Pokud bylo před provedením příkazu y==5 a x==2, platí po provedení příkazu y==3. Hodnota x se nijak nezmění. Mimo popisy postupů v diagramech či v programování na tomhle rozlišování tolik nezáleží, takže taky rovnítka nerozlišujeme.
Černý kroužek je spojka. Nedělá nic, jen spojuje přicházející čáry, pokračuje se z něj tou třetí.
Co udělá daný vývojový diagram, pokud na začátku vložíme hodnoty x=12 a y=9?
Pokud o daném postupu dosud nic nevíme, nezbyde, než jej provést, neboli tzv. odkrokovat. Začni v počátečním bloku a krok za krokem postupuj podle diagramu s danými vstupními hodnotami. Neustále sleduj, ve kterém jsi bloku, a jaké jsou hodnoty jednotlivých proměnných. Vyplatí se zapisovat si jednotlivé kroky, nebo aspoň postupně hodnoty proměnných.
| x | y |
|---|---|
| 12 | 9 |
| 3 | 9 |
| 3 | 6 |
| … | |
- Začátek
- Načtení hodnot x=12 a y=9
- x==y neplatí
- x>y platí
- nová hodnota x: 3 (12-9)
- x==y neplatí
- x>y neplatí
- nová hodnota y: 6 (9-3)
- x==y neplatí
- x>y neplatí
- atd.
Řešení
Postup vytiskne hodnotu 3.
Pro jaké vstupní hodnoty je postup algoritmem?
bonus: v podstatě se ptáme na definiční obor funkce Proměnné x a y jsou patrně číselné. Pro vstupní hodnoty 12 a 9 jsme v konečném čase úspěšně dostali jednoznačný výsledek 3. Takže přinejmenším pro tyto vstupy postup algoritmem je. Jak to bude pro jiné vstupy? To je potřeba otestovat. Postupem času si vyvineš cit pro to, které hodnoty jsou podezřelé a vyplatí se na ně zaměřit. Jak pochodíme se dvěma stejnými čísly? Co když bude jedno z nich nula, co když jedna? Co záporná čísla?
Zkontroluj samozřejmě všechny vlastnosti algoritmu. Brzy zjistíš, že jediný problém je pro některé vstupy s konečností.
Řešení
Postup skončí, pokud jsou obě vstupní hodnoty stejné, nebo pokud jsou obě kladné.
Pokud je aspoň jedno ze vstupních čísel záporné, bude se větší ze vstupů do nekonečna zvětšovat.
Pokud je menším ze dvou čísel nula, bude se donekonečna odečítat od většího čísla (jenže je to nula, takže bez efektu).
Co ten algoritmusTedy daný postup s takovými vstupy, které nevedou k zacyklení. vlastně dělá?
To je téměř detektivní otázka. Štěstí je, že už máš za sebou množství pokusů, takže máš dobrou představu, jak algoritmus pracuje. Pečlivě si uspořádej výsledky do tabulky, např.
| x | 12 | 13 | 14 | 15 | 9 | 12 | 12 | 12 | … |
|---|---|---|---|---|---|---|---|---|---|
| y | 9 | 9 | 9 | 9 | 12 | 10 | 11 | 12 | … |
| Výstup | 3 | 1 | 1 | 3 | 3 | 2 | 1 | 12 | … |
Formuluj hypotézy o vztahu vstupu a výstupu a systematicky je ověřuj. Když se z výsledků zdá, že by nějaká hypotéza mohla být pravdivá, podívej se na vývojový diagram, jestli dává hypotéza smysl i obecně.
Leccos mohou napovědět speciální případy. Co když jsou vstupní hodnoty stejné? Co když se liší o 1, 2, 3, …? Co když je jedna z nich 1, 2, 3, …?
Levý horní roh ještě systematičtější tabulky by vypadal takto:
| x | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | … | ||
| y | 1 | 1 | 1 | 1 | 1 | 1 | 1 | … |
| 2 | 1 | 2 | 1 | 2 | 1 | 2 | … | |
| 3 | 1 | 1 | 3 | 1 | 1 | 3 | … | |
| 4 | 1 | 2 | 1 | 4 | 1 | 2 | … | |
| … | … | … | ||||||
Všímej si: Co se opakuje? Co mají které hodnoty společného? Jak často se objevují nové hodnoty? Které hodnoty jsou nejčastější, které naopak nejvzácnější? Vidíš nějaké vzory? Dokážeš bez provedení algoritmu předvídat výsledek pro nějaký vstup? Jak? Při hledání pravidelností může pomoct barevné odlišování hodnot. Dost práce si ušetří ti, kdo ovládají podmíněné formátování.
Řešení
Vývojový diagram zachycuje Eukleidův algoritmus pro hledání největšího společného dělitele dvou přirozených čísel.
Tvorba vývojového diagramu
Vytvoř vývojový diagram pro výpočet kořenů kvadratické rovnice.
V první řadě si práci rozděl na menší kousky. Je třeba vymyslet samotný postup a následně ho zapsat pomocí vývojového diagramu. Výhoda je, že postup na řešení kvadratické rovnice už ovládáš. Musíš si ho jen trochu promyslet — umět něco udělat ještě neznamená umět to dobře popsat.
- Ujasni si: co všechno je vstupem hledaného algoritmu? Co je výstupem?
- V našem případě se jedná koeficienty rovnice, tedy o reálná čísla tradičně označená jako a, b a c, z nichž a je nenulové.
- Postup znáš. Zkus ho na nějakém příkladu a zapisuj jednotlivé kroky. Zvol si způsob, který ti nejlépe vyhovuje: slovní popis, vývojový diagram na papír či v počítači, nějaká varianta zdrojového kódu…
- Zápis rozšiřuj o jednotlivá rozhodnutí. Musíš pokrýt všechny možnosti, všemožné kombinace vstupních hodnot.
- Pokud je zápis hotový, otestuj ho. Podobně, jako jsme v předchozí úloze zjišťovali, co vlastně algoritmus dělá, teď zjištujeme, jestli to dělá správně.
- Pro tvorbu výsledného vývojového diagramu se dobře hodí např. Lucidchart.