Zapisování grafů
- Převádět mezi sebou různé notace a nakreslení grafu.
- Posoudit, pro které grafy se hodí jaká notace (z alespoň dvou, které se naučíme).
- Dobře popsat, jak postupovat při převodech notací a grafů.
Obsah
Grafy potřebujeme i zapisovat, nejen kreslit
Graf nakreslený na papír (nebo na displej počítače) není vždy tou nejlepší volbou:
- Může být příliš velký a složitý, takže místo očekávané přehledosti se spíš zamotáme a uděláme chybu.
- Větší graf rádi necháme ke zpracování počítači, ten si ale s obrázkem moc dobře neporadí.
- Graf můžeme chtít někomu předat, ale ne vždy je to možné v podobě obrázku.
Popsat obrázek dostatečně přesně, aby jej mohl někdo jiný mohl reprodukovat, už jsme zkoušeli. Teď uděláme totéž, ale s grafy. To dost omezuje podobu reprodukovaných obrázků a usnadňuje určení sady obecných pravidel pro popis grafu. Nejdříve se ve dvojici můžete dohodnout na způsobu, jak budete graf popisovat. Potom jeden z vás vybere (nebo vytvoří) graf, který popíše druhému. Měli byste získat dva stejné grafy (předem si rozmyslete, co zde vlastně znamená slovo stejné).
Hru můžete postupně komplikovat:
- Nejlehčí je graf popsat slovy, přirozeným jazykem. Následně můžete přidávat omezení.
- Ten, kdo popisuje, se nebude dívat na toho, kdo kreslí.
- Ten, kdo kreslí, nebude nic říkat, ani se na nic doptávat. Komunikace tedy už nebude vůbec obousměrná, popis grafu by šlo napsat na papír.
- Popis bude využívat jen symbolů, nikoliv slov, aby nezáleželo na jazykových schopnostech toho, kdo kreslí.
- Popis bude využívat jen velmi omezený počet symbolů, např. jen čísla a mezery.
- Použitou abecedu lze omezit ještě víc, až na dva znaky (studujeme informatiku, tak použijeme číslice 0 a 1).
- Jaký "protokol" jste použili? Na čem bylo třeba se dohodnout? Na jaké grafy lze váš protokol použít, a na jaké ne? Co se stane, když ho použijete na nevhodné grafy?
- Komu se daří grafy posílat nejrychleji? Proč?
Způsob kódování grafu označujeme také pojmem grafové notace.
Probereme nyní několik základních možností, které jste mohli objevit, a které se v informatice běžně používají. To, na čem jste se s protistranou dohodli, byl váš způsob kódování grafu. Prozkoumáme teď několik způsobů, které běžně používají informatici. Všímejte si, v čem se s vaším způsobem shodují, a v čem se naopak liší.
Potřebujeme najít způsob, jak graf zakódovat pomocí dané množiny znaků (např. 0 a 1). Připomeňme si, že je celkem jedno, jak je graf nakreslený co do tvaru nebo velikosti. Důležité je, které vrcholy jsou spojeny se kterými, grafy reprezentují strukturu vztahů.
Otevřete si stránku s jednoduchým appletemJednoduchý jednoúčelový program, který běží v rámci jiného programu, např. ve webové stránce v prohlížeči. http://g.ivank.net/.
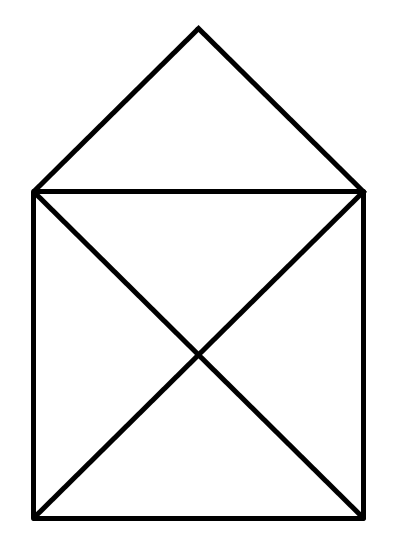
Zkonstruujte pomocí appletu známý graf „domeček“. Najděte způsob, jak učiteli snadno ukázat, že se to povedlo (aniž by se musel přijít podívat).
Zkuste sestrojit i další grafy.
Způsob popisu grafu, který jste právě poznali, se nazývá seznam hran. Potvrdili jsme si, že i na první pohled těžko uchopitelnou strukturu bez začátku či konce, jako je graf, můžeme reprezentovat pomocí posloupnosti znaků.
- Kolik má graf domečku vrcholů? Vidíme to všichni stejně?
- Došli všichni ke stejnému řešení, tedy ke stejnému zápisu grafu domečku?
- Jestli ne, čím se zápisy liší?
- Zkuste hledat alternativní zápisy pro různé grafy. Na čem závisí jejich počet?
- A naopak: odpovídá libovolnému seznamu hran právě jeden graf?
Vraťte se na stránku s appletem http://g.ivank.net/.
- Zkonstruujte pomocí appletu domeček, tentokrát ale s poněkud jiným tvarem, např. se špičatější, plošší nebo šikmou střechou (aniž byste vrcholy grafu posouvali ručně).
- Vymyslete a popiště, jak pomocí appletu graf domečku sestrojit co nejúsporněji (na co nejméně kliknutí a stisků kláves).
Matice sousednosti
Seznam hran může být jako kódování dost "upovídaný". Zabere hodně místa, takže např. trvá dlouho ho odvysílat. Podívejme se, jestli by nešlo vymyslet úspornější kódování (zápis grafu pomocí znaků, obvykle čísel). Nejlíp rovnou pomocí jedniček a nul, ať hned vidíme náročnost v bitech.
Otevřete stránku Graph Online a doplňte do levé části jedničky a nuly tak, aby se po stisku tlačítka Plot graph zobrazil náš známý domeček.
Musíte odhalit, jak kódování funguje. Nebojte se experimentovat.
Princip matice sousednosti je tedy podobný: řádky a sloupce odpovídají vrcholům, a v buňkách je jednička, pokud odpovídající vrcholy sousedíJsou spojeny hranou; odtud také název matice sousednosti., a nula, pokud ne. No a to je celé. Navíc se můžeme domluvit na konvenci, že se nebudeme starat o označení vrcholů. Prostě je budeme číslovat od jedné.
Dekódujte a nakreslete (rukou či na počítači) tento graf:
0110000 1010011 1101010 0010101 0001010 0110100 0101000
Porovnejte svoje řešení s dalšími. Jsou stejná? Čím se liší? Je některé chybně?
- Odpovídá každému grafu právě jedna matice?
- Odpovídá každé matici právě jeden graf?
Skóre grafu
Další způsob popisu grafu se nazývá skóre. Je to posloupnost tzv. stupňů jednotlivých vrcholů.
Stupeň vrcholu je počet jeho hran (v orientovaném grafu proto rozlišujeme vstupní a výstupní stupeň, tedy počet hran vedoucích „dovnitř“ a počet hran vedoucích „ven“). V pražském metru je stupeň Černého Mostu 1, Malostranské 2, Florence 4. Stupeň většiny křížení v pavoučích sítích je 4. Sjezd z dálnice má vstupní stupeň 1, výstupní 2. Stejně na tom jsou dotazy v rozhodovacím stromě (pokud umožňují právě dvě odpovědi).
Úkoly:
- Napište skóre grafu z předchozího úkolu (domeček, bez vrcholu uprostřed, prostředek berte jako křížení hran).
- Nakreslete jiný graf se stejným skóre. Je opravdu jiný? Nebo je jen „pokroucený a zpřeházený“, ale vlastně stejný? Aha!
- Skóre je navíc mnohem kratší než seznam hran! Bylo by tedy možné používat skóre jako úspornějšíÚspornější co do počtu použitých znaků, tedy zabrané paměti. Samozřejmě pak je náročnější graf dekódovat, tedy podle skóre nakreslit. způsob kódování grafu? Rozmyslete, jaké vlastnosti takové kódování musí mít, aby bylo použitelné, a prozkoumejte, jestli tyhle vlastnosti skóre splňuje. Vysvětlete a zdůvodněte svůj závěr. Jestli potřebujete, použijte různé ukázkové grafy apod.
Čím je určen graf?
V předchozích aktivitách jsme se oprostili od spojení grafu a jeho konkrétního nakreslení. Potřebovali jsme přenést či zakódovat jen to, co je na grafu opravdu podstatné. Díky tomu už víme, co to je.
Graf je jednoznačně určen svými vrcholy a jejich propojením hranami.
Proč je třeba určit i vrcholy, když stejně popisujeme jejich propojení hranami?
Další informace?
Graf je definován svými vrcholy a hranami mezi nimi. Někdy ale situace vyžaduje pracovat s dalšími podrobnostmi. Např. v úloze s výletem na kopec bylo třeba počítat s délkami jednotlivých úseků. Za tím účelem ke grafům přidáváme tzv. ohodnocení hran či vrcholů. Zpravidla je to číslo, které se váže k dané hraně či vrcholu. Může jít o délky cest, propustnosti datových linek, dlužné částky mezi zeměmi, doby trvání úkolů a mnoho dalšího. Nemusí jít ale jen o čísla, často máme např. pojmenované vrcholy. V případě rozhodovacích stromů mají některé vrcholy přiřazenu otázku, hrany mají směr a odpověď. S ohodnocenými grafy můžeme řešit ještě mnohem širší škálu problémů.
Pracujeme-li se zakódovanými grafy, často se přirozené místo pro ohodnocení přímo nabízí. V seznamu hran můžeme ohodnocení hran připojit přímo ke dvojici vrcholů, která tu kterou hranu určuje. V matici pak můžeme na místo 0 a 1 psát přímo dané ohodnocení (a nějakou speciální hodnotou vyjádřit, pokud daná hrana vůbec neexistuje). V každém případě si také můžeme vytvořit vedle ještě jeden seznam a do něj zaznamenat ohodnocení jednotlivých vrcholů či hran.
Pracujeme-li s grafy nakreslenými, píšeme ohodnocení zpravidla přímo k dané hraně či vrcholu.
Někdy můžeme ohodnocení reprezentovat i jinak a vytvořit tak užitečné vizualizace.
Doplňující otázky a úkoly
Představte si, že byste matici dostali opravdu jako pouhý sled bitů:
- 0110000101001111010100010101000101001101000101000
Nemůžete začít kreslit, dokud se nevyjasní, kde začínají a končí jednotlivé řádky. Takže: Co s tím?
Vyberte si jednu ze dvou možností (nebo vymyslete ještě jinou):
- Vykoukat velikost nějakým kouzlem (?) přímo z datové zprávy, tak jak je.
- Velikost ke zprávě přibalit. neboli: Jakým způsobem přidat počet vrcholů ke zprávě obsahující matici po řádcích? Pozor: Musí to fungovat pro libovolně velké grafy. Nemůžete se spolehnout, že posílané číslo bude mít méně, než třeba 3 číslice.
Jaké jsou výhody a nevýhody uvedených přístupů?
Který způsob zápisu grafů je lepší? To záleží, co zrovna potřebujeme, na čem nám v dané situaci záleží. Málokdy existuje jedno nejlepší řešení pro všechny případy.
U kódování nás velmi často zajímá délka kódu. Je efektivnější seznam hran, nebo matice sousednosti?
- Najděte několik příkladů grafů, které ukáží, že někdy je lepší seznam hran, a někdy matice sousednosti.
- Zjistěte, jak je velikosti grafu úměrné místo zabrané seznamem hran a místo zabrané maticí sousednosti. Velikost grafu obvykle udáváme pomocí počtu vrcholů nebo počtu hran.
- Odpovězte na otázku: pro jaké grafy se lépe hodíZde ve smyslu: je úspornější. seznam hran, a pro jaké matice sousednosti?
Předpokládejte naši obvyklou cvičnou situaci, tedy kódování neorientovaných grafů s vrcholy označenými za sebou jdoucími přirozenými čísly od 1.
- Podívejte se na několik příkladů matic sousednotsti z hodiny. Všimnete si nějaké pravidelnosti, kterou splňuje každá matice? Lze z některé části matice odvodit jiné části? Navrhněte vylepšený způsob, jak kódovat graf pomocí stejné myšlenky jako u matic, a ušetřit přitom místo.
- Zkuste totéž pro seznam hran: je možné jej nějak zestručnit, aniž bychom přišli o podstatné informace?
- Porovnejte komprimované verze obou kódování tak, jako v předchozí úloze: o kolik jsou vylepšená kódování úspornější? Jak jsou délky zakódování úměrné velikosti kódovaného grafu?
je lepší změnilo se nějak, čemu jsou
Závěr
Graf je přehledný a praktický, pokud potřebujeme pracovat se vztahy. Na druhou stranu, když je graf velký, je potíž jej zakreslit a dále zpracovávat ručně. V takové situaci (a takových situací je většina) graf vhodně zakódujeme a k jeho zpracování využijeme počítač. Jednoznačný způsob zakódování nám mimo jiné umožní zpracovávat grafy automatizovaně. Popsat, jak spočítat např. počet vrcholů a hran daného grafu, je jednodušší, pokud máme v rukou (či v souboru) seznam hran či matici sousednosti, než obrázek.