Úvod
- Co a k čemu jsou modely.
- Co a k čemu jsou grafy (v informatice).
- Jakými pojmy o grafech mluvíme.
- Odhadovat co je v zadání podstatné pro řešení problému a co nikoliv.
- Modelovat pomocí grafů různé situace a řešit různé problémy.
Úvodní úlohy
Utvořte skupinky a vyřešte některou z následujících úloh. Připravte se vaše řešení předvést ostatním. Budete mít omezený čas, soustřeďte se na stručnost a zároveň přesvědčivost vašeho vystoupení. Zvažte (v souladu s pokyny učitele), jestli vaše sdělení podpoří nějaké kreslení na tabuli či promítnutí několika obrázků či slajdů (musí ale být jednoduché, abyste je stihli připravit).
Z chaty na východní úpatí je to 2 km, na západní úpatí 3 km, na jižní úpatí ke stanici lanovky 5 km. Z východního úpatí na vrchol je to 4 km, ze západního 5 km. Na jižním se nastoupí na lanovku dlouhou 700 m a od lanovky se jde na vrchol už jen 500 m. Pěšky z jižního jsou to 2 km prudkým stoupáním. Z chaty se dá jít taky údolím k heliportu (4 km). Odtud se doletí buď 1 km od vrcholu, nebo přímo k dolní stanici lanovky.
Jak se batůžkáři Adam, Barbora a Marie dostanou z chaty na vrchol tak, aby při tom našlapali nejméně kilometrů?
Zkuste si situaci nějak znázornit. Uvažujte při tom, co je a co není pro řešení důležité. Můžete jednotlivá místa zakreslit, spojit cestami a připsat jejich délky. Pomůže, když jsou délky cest v poměru se zadáním, ale není to nutné. Zjistíte, že cest na vrchol není mnoho a nemáte-li lepší nápad, můžete je systematicky prověřit.
Řešení
S pomocí obrázku lze prostým zkoušením celkem rychle najít nejkratší cestu, přičemž slovem „nejkratší“ máme na mysli délku chození (lanovka ani vrtulník se tedy nepočítají). Jiná věc je dokázat, že nalezená cesta opravdu nejlepší je a že jsme nic nepřehlédli. V jednoduchých případech nám k tomu naštěstí pomůže rozbor všech případů, tedy všech možných cest z chaty na vrchol. Díky nákresu můžeme snadno postupovat systematicky.
V podzemním výrobním zařízení hlídá v noci strážný. Zařízení tvoří místnosti spojené různě dlouhými chodbami. Strážný musí pravidelně všechny chodby projít. Z vrátnice vede po jedné chodbě do šatny, skladu i kantýny. Mezi skladem a kantýnou je přímá chodba. Ze šatny vedou chodby do všech ostatních místností. Do dílny se lze dostat kromě šatny také ze skladu.
Najdete pro strážného takovou trasu, aby na ní prošel všechny chodby právě jednou? Lze to udělat tak, aby obchůzku skončil na stejném místě, kde ji začal? Existuje takových tras víc?
Zkuste si situaci nějak znázornit. Všimněte si, že úloha obsahuje více než jednu otázku. Přinejhorším lze vyzkoušet všechny možnosti. Pokud se nějakou chvíli nedaří, uvažte, jestli úloha vůbec nějaké řešení mít musí.
Řešení
Trasu najít lze, například z vrátnice přes kantýnu, a sklad znovu do vrátnice, odtud pak do šatny, skladu a dílny, znovu šatny a skončit v kantýně. Existuje i mnoho dalších možností. Pokud bychom ale chtěli, aby se strážný ještě v rámci obchůzky vrátil na místo, odkud vyšel, nepořídíme. Zdůvodnit to můžeme rozborem (a vyloučením) jednotlivých potenciálních možností s pomocí několika logických úvah. Na tuto problematiku se brzy podíváme i podrobněji.
Z plynárny a elektrárny je třeba rozvést plyn a elektřinu do tří různých měst. Vodu čerpají přímo ze studní, splašky je ale třeba svést do čističky. Aby se snížilo riziko poruchy či výpadku, je dobré všechna vedení umístit do země a tak, aby se nikde nemusela křížit. Vedení mohou zatáčet, ale nevětví se. Musí vést vždy přímo, nikoliv přes jiné město.
Navrhněte rozmístění zařízení, měst a vedení.
Pomohlo by případně některá zařízení (nebo města) postavit jinam?
Asi budete potřebovat více pokusů — použijte tužku a gumu, nebo vhodný editor. Postupujte systematicky, abyste zbytečně nezkoušeli stejnou možnost několikrát.
Řešení
Daná propojení rozvrhnout nelze, a to ani s případným jiným rozmístěním měst a zařízení. Můžete se o tom přesvědčit pečlivým rozborem všech případů. Ať už budete postupovat jakkoliv, vždy uzavřete z jednotlivých vedení okruh, přičemž nějaké další vedení by ho muselo protnout (např. když zbude elektrárna uvnitř okruhu a neelektrifikované město vně).
Naznačeným způsobem se pochopitelně neřeší žádná skutečná vedení. Obdobné problémy se nicméně řeší při navrhování elektrických obvodů (přinejmenším z výrobních důvodů je velmi vhodné, aby se vešly na plochu a bez křížení).
Bořek má dvojčata, syna Adama a dceru Gábinu. Daniela má dceru Zuzanu a již odrostlejšího syna Jana. Hanka je ženou Bořka. Cecil je manželem Ilony. Hančin přísný otec je Cecil, Ilonin otec se jmenoval Karel. Karel byl zároveň dědečkem Daniely. Celá rodina žije v jednoduchém světě, kde se neopakují jména a nestřídají partneři.
V jakém vztahu jsou Adam a Daniela?
Zkuste si situaci nějak znázornit. Můžete použít i nějaký software, čímž si usnadníte změny polohy členů rodiny. Nemusíte tedy gumovat a překreslovat pokaždé, když netrefíte správné generační vztahy.
Řešení
Šablona:Claar Jak vidno, Daniela je Adamovou tetou, Adam je Danieliným synovcem. Obrázek jsme vytvořili pomocí služby Family Echo.
Sníh zaskočil silničáře a ti se snaží co nejdřív opět zprovoznit síť městských ulic. Město je tvořeno dvanácti čtvercovými bloky domů, vchody jsou vždy na rozích bloku. Bloky jsou uspořádány ve třech řadách a čtyřech sloupcích. Za zprovozněnou prohlásíme takovou síť, ve které se lze od každého vchodu (na rohu některého bloku) dostat ulicemi do libovolného jiného vchodu (třeba i oklikou).
Které úseky ulic (mezi dvěma křižovatkami) je třeba protáhnout, aby byla síť zprovozněna? Kolik úseků to je? Silničáři samozřejmě nechtějí protahovat nic navíc, naopak potřebují, aby byla síť co nejdříve zprovozněna. Existuje více řešení? Pokud ano, které z nich je nejlepší, proč?
Zkuste si situaci znázornit obrázkem. Asi není problém najít nějaké řešení, jak ale odhalit to, které vyžaduje nejméně odklízení?
Řešení
Ať už se silničáři rozhodnou zprovoznit síť jakkoliv, vždy musí protáhnout aspoň 19 úseků z 31. Zároveň to stačí — kdyby protáhli byť jediný úsek navíc, jen by uzavřeli nějakou smyčku, nepropojili by ale žádné domy, které dříve propojeny nebyly. Na obrázku vidíte některé z mnoha variant řešení. Uprostřed je síť zcela bez sněhu.
Co do počtu protažených úseků se jednotlivá řešení neliší. Lze přesto říci, že by některá byla lepší než jiná? Proč?
Uspořádat výlet s kolektivem dospívajících není vždy jednoduché. Chtěli bychom co nejvyšší účast, jenže: Adéla nepojede, pokud pojede Hanka nebo Eva. Hanka a Eva rozhodně nepojedou zároveň. Naopak Běta a Cyril pojedou jedině spolu. Běta se ovšem nesnese s Danielou. Gábina se přátelí se všemi kromě Hanky.
Kolik nanejvýš lidí z popsané skupiny lze dostat na společný výlet? Kdo na výlet pojede?
Zkuste si situaci nějak přehledně znázornit. Z dobrého znázornění už se dost jasně vyjeví, kdo by jet měl, a naopak čí účast nestojí za to, protože zabrání většímu počtu dalších účastníků.
Řešení
U téhle úlohy je nejtěžší nalézt způsob reprezentace situace tak, abychom se v ní vyznali. Nakresleme si schéma s jednotlivými potenciálními účastníky a vztahy mezi nimi. Spojíme čarou ty, kteří na výlet nemohou společně. Na výsledném obrázku pak vybíráme co největší skupinu lidí tak, že žádní dva nejsou propojeni (protože propojení znamená, že spolu nemohou jet). Díky obrázku hned vidíme, že vlastně řešíme dvě nezávislé podskupinky, což dost usnadňuje řešení. Celkem mohou jet nanejvýš čtyři účastníci, lze je vybrat dvěma způsoby.
Jak jste si poradili s Bětou a Cyrilem? Běta pojede, právě když pojede Cyril, a tím pádem na sebe vzájemně přenášejí i (ne)kamarádské vztahy k dalším lidem. Zdvojením všech takových vztahů (pro Cyrila i Bětu) zajistíme, že v nejlepším řešení vždy zahrneme oba dva, nebo ani jednoho. Z hlediska sítě vztahů jsou vlastně oba zcela stejní. To vede informatika ke zpřehlednění: prostě je spojí do jednoho bodu v síti, který ale bude počítat za dva.
Takovéto úlohy patří mezi nejobtížněji řešitelné. S větším počtem účastníků a složitějšími vztahy nemusí být v rozumném čase vůbec řešitelné.
Tak kde jsou ty grafy?
Všimli jste si, co mají uvedená řešení společného? Mnoho z nich využilo nějaká shémata či nákresy. Jednotlivé úlohy se přitom vzájemně velmi lišily. Setkali jste se s podobnými schématy či nákresy i v jiných souvislostech? Zdá se, že jsou takové obrázky využitelné ve velmi rozličných situacích. Pojďme se na ně podívat blíž.
Grafem v informatice rozumíme strukturu propojení dvojic nějakých objektů. Nejjednodušší je představit si příklad. Nějaké jste viděli v předchozích úlohách, zde přidáme nějaké další.
Příklad: Grafy v různých souvislostech
Uvažujte:
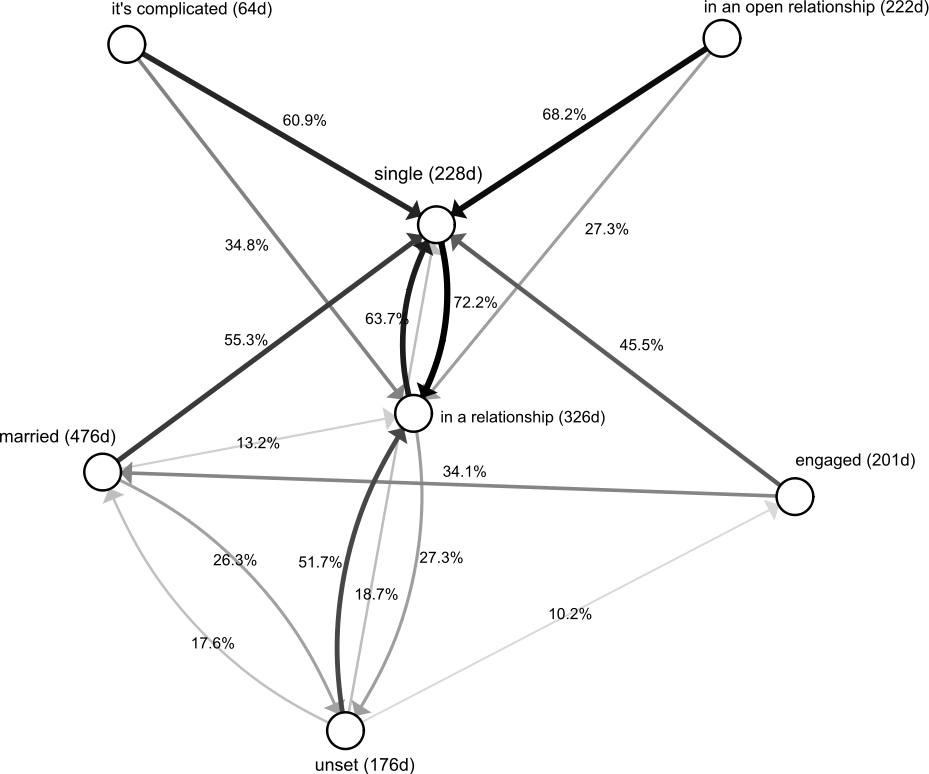
- Co znamenají uvedená procenta, z čeho se počítajíProcenta udávají podíl přechodů z daného výchozího stavu do jednotlivých cílových stavů. Z obrázku např. vyčteme, že 60.9 % stavů „it's complicated“ se změní na stav „single“.?
- Mají nějaký význam tloušťky, resp. barva čarOdpovídají uvedeným procentům, usnadňují identifikaci nejčastějších přechodů.?
- Co jsou ta čísla u jednotlivých stavůVyjádření délky trvání stavu ve dnech. Trvání se samozřejmě v jednotlivých případech liší, proto je zobrazen medián („poločas“).?
- Chybí v obrázku něcoNapříklad přechody s pravděpodobností pod 10 %. A samozřejmě se jedná jen o výsek části uživatelů v omezeném čase.? Napadá vás pročCílem obrázku je přehlednost, méně důležité přechody je proto lepší vynechat.?
- Jak to, že např. do stavu „single“ přechází víc než 100 % ostatních stavů, není to nějaký nesmyslNení, procenta vypovídají o opouštěných, nikoliv o cílových stavech.?
- Vidíte nějaké zajímavostiNapříklad je zajímavé, že zasnoubení končí častěji rozchodem než manželstvím, nebo že méně než 10 % vztahů končí zasnoubením (jinak by byl zobrazen příslušný přechod).?
Grafy nám umožňují získat lepší přehled než například slovní popis situace. Umožňují nám abstrahovat od toho, co není důležité, a naopak se soustředit na to, co je pro naši úlohu či situaci určující. Další výhodou je možnost systematického prozkoušení všech možností řešení — to by šlo podle slovního popisu dost těžko.
Grafy slouží k modelování situací, kde záleží na vzájemných vztazích.
Modely
Model je reprezentace skutečnosti, která vynechává, co není důležité, a naopak zachovává, co důležité je. Smyslem modelu je zjednodušt jinak komplikovaný problém a soustředit se jen na to podstatné. Různé nástroje k modelování již znáte. Model terénu je třeba mapa, z psychologie znáte modely lidské motivace. Množiny používáme k modelování skupin, přirozená čísla k modelování jejich velikosti a reálná čísla k modelování vzdáleností. Z chemie a fyziky znáte různé modely atomu. Přitom už víte, že třeba ten model atomu není přesným popisem skutečného atomu, je jen popisem dostatečně přesným. Všichni znáte pokyn „tření a odpor vzduchu zanedbejteU většiny školních úloh je opravdu zanedbat můžete. Víte ale třeba, při jakých rychlostech je už odpor vzduchu nezanedbatelný?“.
Modelování nám umožňuje vůbec porozumět světu, aniž bychom o rozum přišli. Jakékoliv naše představy o světě jsou vždy právě jen modely, protože o něm nedovedeme získat dostatek dostatečně přesných informací. Schopnost abstrakce (tedy poznat, co je důležité, a pominout to ostatní) je jedna z nejcennějších, kterou si ze školy máte odnést.
Vraťte se k některé z úvodních úloh a pojmenujte, co je pro řešení důležité a potřebujeme to do grafu zahrnout, a co důležité není, a nemusíme se tím zabývat. U každé úlohy je to něco jiného.
Příklad řešení — Batůžkáři
U úlohy s batůžkáři nás zajímá, mezi kterými místy existuje spojení, a kolik se na něm turista nachodí. Naopak nás nezajímá konkrétní fyzická poloha jednotlivých míst, jak je který úsek strmý, ani jména účastníků výletu.
Slovníček
Během dosavadní práce s grafy jste možná pocítili potřebu některé věci pojmenovat. Zde nabízíme pro zajímavost přehled několika základních pojmů souvisejících s grafy. Nejedná o definice, spíše o vysvětlení. Není také nutno si je všechny hned zapamatovat. Na to si uděláte čas, až budete ten který pojem potřebovat.
Uhodnete, proč používáme právě označení vrcholy a hrany?
- Vrcholy (uzly)
- „Body“ v grafu, to, co se spojuje hranami. Vrcholy představují objekty, jejichž vztahy modelujeme.
- Hrany (spoje)
- „Čáry“ v grafu, kterými spojujeme vrcholy. Hrany představují vztahy mezi vrcholy. Hrana je definována vrcholy, které spojuje. Mluvíme proto o hraně A-B, Praha-Brno atp.
- Graf
- Graf je zachycením vztahů mezi objekty. Je tedy definován svými vrcholy (to jsou ty objekty) a hranami mezi těmito vrcholy (to jsou ty vztahy). Z předchozí věty mj. plyne, že je úplně jedno, jak je graf nakreslený, nebo jestli je vůbec nakreslený. Záleží jen na struktuře vztahů. Dva grafy obsahující stejné vrcholy a stejné hrany jsou stejné. Podobně platí 1 = 3⋅ ⅓ = 0,9, hodnota se jiným zápisem nijak nemění. K této skutečnosti se ještě vrátíme.
- Ohodnocení
- Někdy potřebujeme k prvkům grafu přiřadit nějaké další informace. Silnice představované hranami mohou být různě dlouhé, hypertextové dokumenty představované vrcholy mají různé adresy apod. Potřebné hodnoty prostě připisujeme poblíž příslušné hrany či vrcholu. Ohodnocení je zpravidla číselné, ale ne nutně.
- (Ne)orientovaný graf
- Neorientovaný graf nerozlišuje směr hran. To jsou např. silnice mezi městy a přátelství na Facebooku. Orientovaný graf směr rozlišuje, na obrázku to většinou značíme šipkou. To jsou např. jednosměrky ve městě a skutečná náklonnost lidí. Má-li být v orientovaném grafu některý vztah symetrický, použijeme prostě hrany dvě, pro každý směr jednu. V naší učebnici obvykle (pokud neřekneme jinak) uvažujeme grafy neorientované.
- (Ne)souvislý graf
- Souvislý graf je „jeden kus“, z každého vrcholu lze po hranách docestovat do libovolného jiného vrcholu. Naopak nesouvislý graf tuto vlastnost nesplňuje, takže obsahuje dvě nebo více tzv. komponent souvislosti: partiček přátel, co se spolu nebaví, fyzicky oddělených počítačových sítí apod.
- Úplný graf
- Graf, ve kterém je každý vrchol spojen hranou (tedy přímo) s každým jiným vrcholem.
- Stupeň vrcholu
- Počet hran s jedním koncem v daném vrcholu. Typická křižovatka má stupeň 4, křižovatka tvaru T má stupeň 3. Pokud je graf orientovaný, rozlišujeme vstupní a výstupní stupeň vrcholu.
Kdo si chce hodně namáhat hlavu, uvažuje, jak asi vypadají hypergrafy. V nich hrany nespojují jen dva, ale libovolný počet vrcholů. Geometrická představa už není tak přímočará (žádné jednoduché „body spojené čarami“), hypergrafy nicméně najdou své využití. Lze jimi modelovat např. členství v různých zájmových klubech, kde každá hrana zahrnuje členy jednoho klubu.
Podle situace se někdy hodí uvažovat násobné hrany (z Prahy do Brna mohu po dálnici, nebo vlakem) či smyčky (hrana s oběma konci v tomtéž vrcholu — vzpomeňte např. na tramvajovou smyčku). V této učebnici ale většinou (tedy pokud neuvedeme jinak) násobné hrany ani smyčky uvažovat nebudeme.
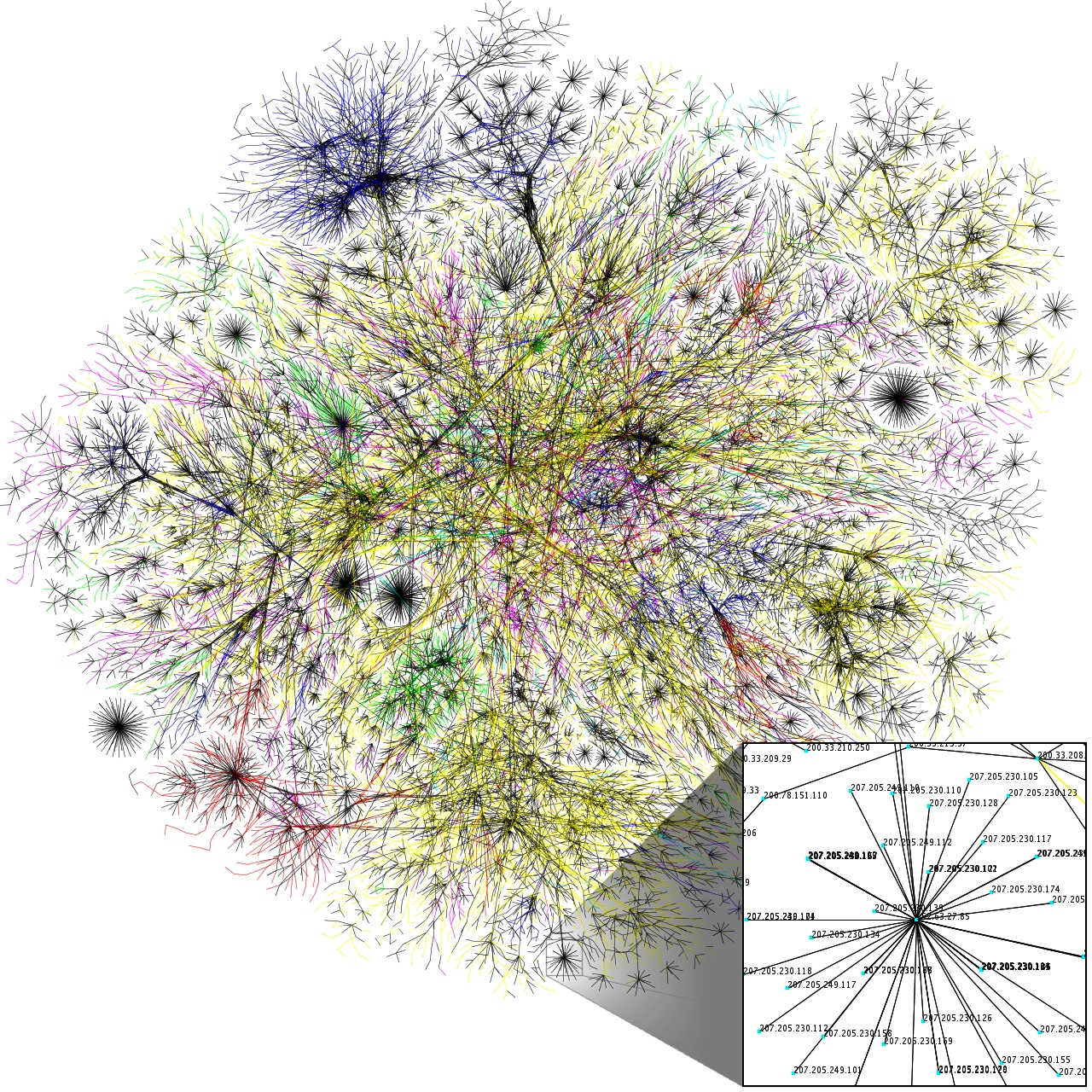
O grafech je toho mnoho vyzkoumáno, což je další výhodou jejich použití v rozličných situacích. Když už situaci zachytíme pomocí grafu, můžeme graf známým způsobem zapsat do počítače a použít na něj nějaký už známý postup zpracování . Například hledání nejkratší cesty mezi dvěma vrcholy grafu funguje zcela stejně, nezávisle na tom, jestli jde o graf mravenčích chodeb, internetových spojení nebo metabolismu.
Příklad: Strážný řečí grafů
Na podzemním výrobním zařízení nás zajímají místnosti a jejich propojení chodbami. Místo výrobního zařízení proto budeme pracovat s grafem, jehož vrcholy představují jednotlivé místnosti a hrany odpovídají chodbám. Hrany grafu nejsou orientované, chodbami lze procházet oběma směry. Naším úkolem je pak najít navazující posloupnost všech hran. V ní jsou všechny hrany (právě jednou) seřazeny tak, aby konec jedné hrany byl začátkem hrany následující, tedy aby hrany odpovídaly hledané trase strážného.
Formulace problému řečí grafů mimo jiné usnadní hledání souvislostí s jinými problémy a přizpůsobení již známých řešení. Např. strážný řeší podobný problém, jako pošťák, který má nejspíš dopis pro téměř každý dům ve svém rajónu, a samozřejmě se nechce zbytečně nachodit.
Shrnutí
- Model je zjednodušení reality, které vynechá její nepodstatné aspekty, čímž zpřehledňuje situaci. Příkladem modelu je planetární model atomu nebo plán městské hromadné dopravy.
- Každý model je ze své podstaty nepřesný. Pokud jsme ale model nezjednodušili příliš, není nepřesnost na škodu.
- Veškeré naše uvažování probíhá prostřednictvím modelů, na celou realitu ani nemáme mozkové kapacity.
- Graf je abstraktní struktura, která zachycuje vztahy mezi dvojicemi objektů.
- Mezi základní příklady patří modelování sítě silnic spojujících města či sociální sítě vzájemných přátelství. Vrcholy grafu budou představovat města (resp. lidi), hrany budou představovat silnice (resp. „přátelství“).
- Grafy mohou usnadnit řešení problému tím, že jej přehledně znázorní.
- Další výhodou je možnost použití již známých postupů, není tak nutno řešit každý problém znova od začátku.