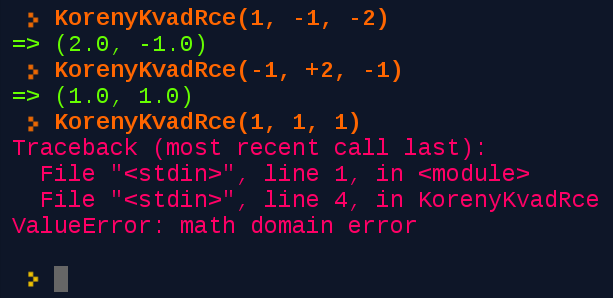
Počítač za mě dělá jednoduchá rozhodnutí

Co se naučíš:

• Nechat program samostatně rozhodovat o dalším postupu podle předem daných pravidel.
• Rozlišovat mezi dvěma různými významy rovná se.
• Pracovat v Pythonu s pravdou, nepravdou a logickými výrazy.
• Díky možnosti rozhodování tvořit univerzálnější funkce a tím si ušetřit ještě více práce.

Příklad: Řešení kvadratické rovnice jednoduše

Kvadratická rovnice se uplatní v souvislosti s pohybem těles v gravitačním poli.

Zkusme si naprogramovat pomůcku pro výpočet kořenů kvadratické rovnice. Tedy rovnice ve tvaru , kde a, b a c jsou dané konkrétní parametry, x je neznámá a my hledáme takovou její reálnou hodnotu, aby rovnice platila. S takovou rovnici se setkáme při řešení řady různých problémů, např. v analytické geometrii (takže i v počítačové grafice) nebo při pohybu tělesa v gravitačním poli (takže i při modelování virtuální reality).

Smyslem úkolu je, abychom nemuseli pořád dokola počítat vlastně totéž, jen s jinými hodnotami. Chceme zadat jen potřebné parametry a počítač už by spočetl výsledek. S trochou znalostí z matematiky bychom mohli přijít třeba s takovouto funkcí:

import math
def KorenyKvadRce(a, b, c) :
	Diskriminant = b**2 - 4*a*c
	Koren_1 = (-b + math.sqrt(Diskriminant)) / (2*a)
	Koren_2 = (-b - math.sqrt(Diskriminant)) / (2*a)
	return Koren_1, Koren_2

Rozmysli si:

• Proč nemůžeme ve výpočtu diskriminantu napsat prostě přímo 4ac jako v matematice, proč píšeme 4*a*c?
• Proč je lepší napsat jmenovatel 2*a do závorky?

Úloha: Zkouška funkce

Vyzkoušej (např. v interaktivní konzoli) uvedenou funkci pro rovnice:

• 
• 
• 

Odpovídají výsledky tvým očekáváním?

Nápověda

Kořeny rovnice hledáme spuštěním KorenyKvadRce(1, -1, -2) v konzoli.
Nezapomeň na import matematického modulu (import math).

Řešení

Výsledky pro dané kvadratické rovnice. Vysvětlení opět poskytuje poslední řádek. Domain v tomto kontextu odpovídá českému termínu obor hodnot.

Jestli rozumíš kvadratickým rovnicím, možná už tušíš, kde nastala chyba. Některé kvadratické rovnice nemají reálné kořeny. Při „ručním“ výpočtu to poznáme podle hodnoty diskriminantu. Podle jeho hodnoty rozlišíme, jestli má rovnice dva, jeden, nebo žádný reálný kořen. Naše funkce ale nic takového nedělá. Při pokusu o odmocnění záporného diskriminantu pak dojde k chybě.

K zabránění této chybě ale není potřeba žádný lidský asistent, pravidlo je jasné: rovnice se záporným diskriminantem nemá žádný reálný kořen. Zachovat se podle takhle jednoznačného pravidla Python musí zvládnout, jinak by nám nebyl moc užitečný.

Rozhodování: if a else

Než budeš pokračovat dál, vytvoř si vývojový diagram pro hledání kořenů kvadratické rovnice.

Nejdřív promyslet řešení rovnice, potom programovat

Situaci dost usnadní, když už studenti budou mít s kvadratickou rovnicí a jejím řešení aspoň krátkou předchozí zkušenost. Velmi vhodné je také nejdřív sestavit vývojový diagram a až poté zde zkoumat, jak vlastně řešení rovnice naprogramovat.

Příklad: Opravené řešení kvadratické rovnice

Naši funkci tedy upravíme:

Komentáře

Všimni si textu # rovnice nema koren. To je tzv. komentář. Python jej ignoruje, slouží totiž lidem k usnadnění porozumění zdrojovému kódu. Cokoliv je na řádku za znakem # je Pythonem považováno za komentář. Ve sbírce zdrojových kódů, které přidáváš ke svým zápiskům z hodin informatiky, je užitečné pomocí komentářů zapsat vysvětlení, co která část programu dělá, jak a proč.

1 def KorenyKvadRce(a, b, c) :
2     Diskriminant = b**2 - 4*a*c
3     if Diskriminant < 0 :	# rovnice nema koren
4         return None		# funkce vrati None, tedy "žádnou hodnotu"
5     else :
6         Koren_1 = (-b + math.sqrt(Diskriminant)) / (2*a)
7         Koren_2 = (-b - math.sqrt(Diskriminant)) / (2*a)
8         return Koren_1, Koren_2

Řádky jsme očíslovali pro lepší orientaci, čísla nejsou součástí zdrojového kódu.

Upravená funkce funguje přesně, jak tušíš: na 3. řádku vyhodnotí, jestli je diskriminant záporný. Pokud ano, provede se následující odsazený řádek (kořen neexistuje, funkce skončí). Pokud podmínka na 3. řádku splněna nebyla, přeskočí program rovnou na 5. řádek s else a provede odsazené řádky pod ním. Všimni si, že některé řádky jsou odsazeny celkem dvakrát. První odsazení značí, že je řádek součástí funkce, druhé odsazení značí, že je řádek součástí rozhodovací větve. Takto Pythonu sdělujeme strukturu programu. Co dané odsazení znamená zjistíme na nejbližším dřívějším řádku, který je odsazen o úroveň méně (schválně si to zkus!).

Uvedený zdrojový kód odpovídá tomuto vývojovému diagramu.

Rozhodování má ve Scratchi stejnou strukturu jako v řadě dalších jazyků včetně Pythonu.

Uvedené konstrukci říkáme rozhodování, větvení, nebo také selekce. Na vývojovém diagramu je přímo vidět, jak se program štěpí na dvě větve podle platnosti podmínky. Tentýž princip opět znáš z tabulkového procesoru (ať už z Excelu nebo odjinud).

Průběh podmíněných příkazů v Pythonu ilustruje oranžový vývojový diagram. Příkazy 1 a 2 se provedou, pokud je splněna Podmínka. Naopak příkazy A a B se provedou, pokud Podmínka splněna není.

Naše funkce pro počítání kořenů kvadratické rovnice má nicméně pořád ještě nějaké nedostatky. Jedním z nich je, že nepozná rovnici s jediným(tzv. dvojnásobným) kořenem. Co myslíš, jak funkce s takovou rovnicí zachází? Pojďme to zjistit.

Úloha: Dvojnásobný kořen kvadratické rovnice

Co přesně dělá poslední verze funkce KorenyKvadRce v případě, že má zadaná rovnice jediný kořen? Můžeš to buď vyčíst přímo ze zdrojového kódu, nebo vyzkoušet (k tomu je třeba mít konkrétní rovnici, tak nějakou sestav; jestli se ti to nedaří z hlavy, můžeš si pomoct úpravou vhodných parametrů v grafu).

1. Co si myslíš, že bude výsledkem volání funkce, a jak k němu funkce dojde?
2. Funkci s příslušnými parametry spusť.
3. Co je výstupem? Jak k němu funkce došla? Odpovídá tvému očekávání?

Řešení

Postupně projdi zdrojový kód a představuj (a zapisuj) si, co se děje při jeho vykonání:

1. V parametrech a, b, c funkce dostane parametry kvadratické rovnice s jediným reálným kořenem.
2. Jako první je spočten Diskriminant. Z matematiky víme, že bude roven nule (plyne to z našeho výběru takové rovnice, která má jediný kořen).
3. Dál funkce vyhodnocuje podmínku, jestli je Diskriminant záporný. To není (je totiž nulový). Program tedy pokračuje větví else na 5. řádku.
4. Tady už se počítá první kořen, tedy Koren_1. Diskriminant je nulový, takže hodnota Koren_1 odpovídá hodnotě výrazu -b/(2*a).
5. Na dalším řádku se spočte Koren_2. Aha! Diskriminant je nulový, takže výsledek výpočtu opět neovlivní a Koren_2 bude roven opět hodnotě -b/(2*a).
6. Nakonec funkce „oba“ kořeny vrátí. To je ale trochu zbytečné, kořeny jsou si rovny, funkce tedy vrací dvojici stejných hodnot.

Rozhodování vnořené v rozhodování

Informatici se snaží o efektivitu. Naše funkce ale v některých případech počítá zbytečně odmocninu z diskriminantu (dokonce dvakrát) a pak stejný kořen navíc spočte ještě jednou. A vrátí dvě stejné hodnoty.

Úloha: Vylepšené řešení kvadratické rovnice

Uprav naši funkci tak, aby nepočítala zbytečně, a vracela v případě potřeby jen jediný kořen.

Nápověda

Jako první je potřeba si rozmyslet, jak vlastně výpočet zorganizovat. Někdo uvažuje „svými slovy“, někdo ve vývojových diagramech, někdo už uvažuje řečí zdrojového kódu. V některém okamžiku se program bude muset rozhodnout, jestli bude počítat jeden kořen, nebo dva. Toto rozhodnutí musíme do programu dopracovat.

Takto by mohl vypadat příslušný vývojový diagram...

Řešení

Jedno z mnoha možných řešení:

 1 def KorenyKvadRce(a, b, c) :
 2     Diskriminant = b**2 - 4*a*c
 3     if Diskriminant < 0 :	# rovnice nema koren
 4         return None
 5     else :
 6         if Diskriminant > 0 :		# rovnice ma dva koreny 
 7             Koren_1 = (-b + math.sqrt(Diskriminant)) / (2*a)
 8             Koren_2 = (-b - math.sqrt(Diskriminant)) / (2*a)
 9             return Koren_1, Koren_2
10         else :				# rovnice ma jediny koren
11             Koren = -b / (2*a)
12             return Koren

Pozorně si jej pročti, prozkoumej a prozkoušej. Všimni si, že druhé if se vyhodnocuje ve větvi else předchozího rozhodování. V programování do sebe různé konstrukce často vzájemně vnořujeme. Programy tak mohou být mnohem složitější (a užitečnější), než jen prostý sled příkazů.

Vývojový diagram uvedeného řešení. Jeho rozložení odpovídá programu, aby bylo dobře vidět, že dělají to samé.

Vícenásobné rozhodování: elif

Příklad: Jednodušší zápis řešení kvadratické rovnice

Někdy se potřebujeme rozhodnout mezí více než dvěma možnostmi. Můžeme samozřejmě hodnocení řetězit a zanořovat, jako v ukázkovém řešení předchozího úkolu. StejněVícenásobným zanořováním funkce, tedy
=KDYŽ(Podminka1;Vysledek1;KDYŽ(Podminka2;Vysledek2;KDYŽ(Podminka3;Vysledek3;...))) bychom postupovali např. v tabulkovém procesoru. Raději ale pro takový případ použijeme klíčové slovo elif, což je zkratka z else a if s významem „pokud není splněna předchozí podmínka, ale je splněna tato podmínka“. Následující zdrojový kód funguje zcela stejně, jako ten v řešení předchozí úlohy:

 1 def KorenyKvadRce(a, b, c) :
 2     Diskriminant = b**2 - 4*a*c
 3     if Diskriminant < 0 :	# tady je prvni podminka
 4         return None
 5     elif Diskriminant > 0 :	# tato vetev se provede kdyz neplati prvni podminka, ale plati tato
 6         Koren_1 = (-b + math.sqrt(Diskriminant)) / (2*a)
 7         Koren_2 = (-b - math.sqrt(Diskriminant)) / (2*a)
 8         return Koren_1, Koren_2
 9     else :			# tato vetev se provede pri neplatnosti vsech predchozich podminek
10         Koren = -b / (2*a)
11         return Koren

Větví elif lze použít kolik je potřeba.

Porovnání hodnot

Někdo by možná chtěl výpočet zorganizovat jinak a v podmínce se rozhodovat podle toho, jestli je Diskriminant roven nule. To je příležitost podívat se na zajímavost, které si v matematice většina studentů nevšimne: některé rovnítko (znak =) má význam „od teď bude hodnota symbolu vlevo rovna hodnotě vpravo“ a některá mají význam „platí, že hodnoty pravé a levé strany jsou si rovny“. Obvykle není potřeba význam rozlišovat (odhalíš důvod?). V programování ale různé významy „rovná se“ rozlišovat potřebujeme.

Úloha: Přirozenější zápis řešení kvadratické rovnice

Předchozí řešení uprav tak, aby lépe odpovídalo obvyklému lidskému postupu. Většinou nejdřív předpokládáme, že je diskriminant kladný a máme dva kořeny. Pokud ne, tak je diskriminant snad aspoň nulový a kořen bude jeden. Rovnice vedoucí na záporný diskriminant jsou ve škole zadávány jen zřídka, vypořádáme se s nimi tedy jako s posledními.

Jednotlivé části rozházeného zdrojového kódu postupně přetáhni do druhého (zatím prázdného) pole. Důležité je samozřejmě jejich pořadí, ale také odsazení.

Řešení

 1 def KorenyKvadRce(a, b, c) :
 2     Diskriminant = b**2 - 4*a*c
 3     if Diskriminant > 0 :	# nejdriv zkousime kladny diskriminant
 4         Koren_1 = (-b + math.sqrt(Diskriminant)) / (2*a)
 5         Koren_2 = (-b - math.sqrt(Diskriminant)) / (2*a)
 6         return Koren_1, Koren_2
 7     elif Diskriminant == 0 :	# potom nulovy - TADY JE OPERATOR POROVNANI
 8         Koren = -b / (2*a)
 9         return Koren
10     else :			# posledni moznost je zaporny diskriminant (neni treba testovat, tady uz je jasne, ze neni kladny ani nulovy, je tedy zaporny)
11         return None

Všimni si v předchozí úloze řádku s podmínkou Diskriminant == 0. Dvojité rovnítko (==) je operátor porovnání. Lze ho číst opravdu jako „hodnota levé strany je rovna hodnotě pravé strany,“ tedy např. „diskriminant je nulový.“ Je to tedy jen tvrzení, které má nějakou pravdivostní hodnotu, není to příkaz a samo o sobě to nic nedělá.

Další užitečné operátory porovnání:

Rovná se	Nerovná se	Větší než	Větší nebo rovno	Menší než	Menší nebo rovno
==	!=	>	>=	<	<=

Jak už víme, jednoduché rovnítko (=) naproti tomu znamená přiřazení. Čteme jej tedy jako „do proměnné vlevo přiřaď hodnotu vpravo,“ např. „Do proměnné Diskriminant přiřaď rozdíl čtverce b a čtyřnásobku součinu a s c.“ Jednoduché rovnítko je instrukce k činnosti a přepisuje hodnotu proměnné vlevo od rovnítka výsledkem výrazu vpravo od rovnítka.

Logické hodnoty a operace s nimi

Ověřování datového typu

Typ „logická hodnota“ v programování se obvykle nazývá Boolean či nějak podobně, např. v Pythonu krátce bool. Proč tak zvláštní označení zjistíš, když vyhledáš, o co se zasloužil George Boole.

Zjistit datový typ hodnoty či proměnné ti pomůže type(Objekt). Zkus do konzole zadat třeba type(2) nebo type(2.0). Datový typ ověřit umožňuje funkce isinstance(Objekt, Typ). Zkus do konzole zadat např. isinstance(True, bool) nebo isinstance(3.0+2.0, int).

Mezi základní typy patří především int (celé číslo), float (číslo s plovoucí řádovou čárkou), bool (logická hodnota), str (textový řetězec, z anglického string), ale třeba také type (tedy datový typ datový typ, např. int, float, bool, str, type…).

Už jsme zmínili, že datovým typem může být také logická hodnota (True nebo False), tedy pravdivostní hodnota logického výroku.

Rozhodovací podmínka„to mezi if a dvojtečkou“ je v zásadě jakýkoliv výraz, který lze vyhodnotit právě na True nebo False. Schválně zkus do interaktivní konzole zadat třeba:

• 1 < 2
• 18 == 20 - 2
• 2**10 == 1024
• (((2**2)**2)**2) == (2**(2**(2**2)))

V rozhodovacích podmínkách obvykle využíváme buď porovnání nějakých hodnot, nebo výsledek volání funkce, která logickou hodnotu přímo vrací (pomocí slova return).

Tak jako s čísly můžeme provádět číselné operace (pomocí operátorů +, -, atd.), s logickými hodnotami můžeme provádět operace logické. Zkus do konzole zadat třeba:

• True and True
• False and True
• False or True
• not True

Zkontroluj, jestli se logické operátory and, or a not chovají správně podle očekávání. Šel by operátor porovnání využít jako logická ekvivalence? Pokud ano, můžeš si ověřit i složitější logické výroky, třeba not (P and Q) == (not P) or (not Q). Předtím samozřejmě musíš zadat nějaké hodnoty proměnným (např. P = True, Q = True). Ověř platnost výroku pro všechny kombinace hodnot P a Q. Jak to udělat co nejjednodušeji?

Tohle všechno si nemusíš hned pamatovat. Potřebuješ ale vědět, že to existuje, a že to tady (nebo jinde) v případě potřeby najdeš. Pokud budeš programovat pravidelně, zapamatuješ si vše potřebné prostě častým používáním.

Další úlohy a příklady

Úloha: Větší ze dvou čísel

Klasickou úvodní úlohou na rozhodování je funkce vracející největší ze dvou parametrů. Např. volání Vetsi(45, 37) má vrátit hodnotu 37. V textovém poli vidíš rozpracovanou funkci: už má hlavičku (určené jméno a parametry), a je jasné, že bude vracet jeden z nich. Navíc jsou připraveny testovací výstupy, na kterých hned uvidíš, jestli funkce pracuje správně.

Dokonči funkci Vetsi tak, aby vracela hodnotu největšího ze dvou parametrů. Jak myslíš, že by se funkce měla zachovat, když jsou obě zadané hodnoty stejné?

Řešení

Jedno z možných řešení:

def Vetsi( a, b ) :
   if a > b :
      return a
   else :
      return b

Pokud jsou obě hodnoty stejné, je pravděpodobně jedno, kterou z nich funkce vrátí (a ze zadání nic přesnějšího neplyne). Někdy ale očekáváme, že je jedna z hodnot ostře větší. V takovém případě by měl program při shodě hodnot nahlásit chybu. Informatici si vždy pečlivě hlídají rozdíl mezi ostrými a neostrými nerovnostmi.

Úloha: BMI a rozhodnutí o nadváze

Eugenia Martínez Vallejo (také La monstrua desnuda), autor Juan Carreño de Miranda, přibližně 1680

Počítali jsme BMI, abychom zjistili, jestli naše tělo třeba netrpí nadváhou. To rozhodnutí ale není nikterak složité. Jde o prosté porovnání dvou hodnot podle tabulky: BMI nad 25 znamená nadváhu (nebo hůř), BMI pod 25 váhu ideální nebo nižší. Na to je přeci škoda plýtvat vlastním intelektem. Nemohl by to porovnání za nás udělat počítač?

Naprogramuj funkci TrpimNadvahou(Vaha, Vyska). Rozmysli si potřebné detaily: Jaké hodnoty by měla funkce vracet? Co by měla funkce dělat, když je hodnota BMI právě 25?

Nápověda

Postupuj jako obvykle:

1. Rozmysli si, co přesně se po tobě chce.
   1. Funkce má zjistit, jestli daný člověk trpí nadváhou. Může tedy odpovědět dvěma způsoby které dobře odpovídají logickým hodnotám True (trpí nadváhou) a False (netrpí). Právě takové hodnoty tedy budeme vracet.
   2. Trpí nadváhou ten, jemuž vychází BMI rovno 25? To je třeba zjistit a podle toho napsat rozhodovací podmínku. (V případně BMI a nadváhy je vcelku jedno, jak se rozhodneš, nějak se ale rozhodnut musíš.)
   3. Zadání mluví o nadváze, ale asi do ní počítá i všechna vyšší pásma. Jinak by funkce moc nedávala smysl. V případě podobných pochybností je potřeba se obrátit na toho, kdo zadává práci. Měl by vědět, co vlastně chce.
2. Vyzkoušej si daný problém vyřešit na příkladu. Sleduj, jak u toho postupuješ, a jestli tak lze postupovat pokaždé.
3. Svůj postup vhodně popiš: svými slovy, vývojovým diagramem, přibližným zdrojovým kódem...
4. Popis kousek po kousku dále zpřesňuj, až vznikne spustitelný prográmek v Pythonu.
5. Výsledek nezapomeň odladit — tedy testovat a opravovat, dokud se nebude chovat podle tvých očekávání.

Řešení

Jedno z možných řešení:

def TrpimNadvahou(Vaha, Vyska) :
    Index = BMI(Vaha, Vyska)	# funkci na vypocet BMI uz mame, tak nebudeme vzorec zadavat znova
    if Index > 25 :
        return True
    else :
        return False

Další z možných řešení — rozmysli si, že dělá to samé:

def TrpimNadvahou(Vaha, Vyska) :
    return BMI(Vaha, Vyska) > 25

Další testovací hodnoty, které bychom měli otestovat, odpovídají BMI přesně 25. Tedy např.

print(TrpimNadvahou(81, 1.8))

Chová se funkce podle očekávání i pro tento vstup? (Rozhodně by neměla skončit, aniž by vrátila jakoukoliv odpověď!)

Je BMI dobrým indikátorem obezity?

Vztah BMI (indexu tělesné hmotnosti) a podílu tělesného tuku.

Mnoho lidí zajímá, zda nejsou obézní. Jako pomůcku použijí výpočet BMI. Jak ale posoudit, jestli je BMI vůbec dobrý indikátor? Dobrý indikátor dělá málo chyb — jak falešných poplachů (prohlášení svalnatého kulturisty za obézního), tak přehlédnutí. Tak je to s každým jiným testem. Dobrý test na tuberkulózu by měl poznat pokud možno všechny případy tuberkulózy a naopak nestrašit zbytečně zdravé lidi. Kvalitní maturitu by měli složit právě ti, kdo si ji svými dovednostmi zaslouží — nikdo ji nemá získat nezaslouženě, ovšem nikdo ji nemá také nezaslouženě nezískat.

V praxi jsou samozřejmě všechny testy poněkud nepřesné a s danou nepřesností je třeba při interpretaci výsledků testu počítat. Na následujícím obrázku vidíš vynesené lidi podle BMI a podle přímo naměřeného podílu tělesného tuku (ten je jistě přesnějším ukazatelem nadváhy). Jak je na obrázku vidět shoda obou indikátorů?

Podívej se, jak lidi dělí příslušné hranice, tedy nad a pod 25 bodů BMI a nad a pod 25% tělesného tuku. Najdi, kde jsou lidé s nadváhou podle BMI, ale nikoliv podle tuku, a naopak lidé s nadváhou podle tuku, ale nikoliv podle BMI. Popisky na obrázku prozradí, kolik jich je (hodnota N): 1410, resp. 695 z celkových 8550. Tedy celkem skoro 25% špatně zařazených lidí podle BMI.

Je tedy jasnější, jak se na BMI dívat: je to vhodná orientační pomůcka (protože lze velmi snadno spočítat), ale než učiníme nějaké závažné rozhodnutí (třeba o změně životosprávy), je lepší ověřit skutečný stav z dalších zdrojů. Samotná hodnota BMI ještě není důvod ke znepokojení.

Zamysli se: Jak by vypadal obrázek v situaci, kdyby BMI a podíl tělesného tuku byly v užším vztahu a BMI tak mohl sloužit jako přesnější indikátor nadváhy?

Úloha: BMI a zařazení do pásma

Kategorie	Rozsah BMI (v kg/m2)
0	těžká podvýživa	≤ 16,5
1	podváha	16,5 – 18,5
2	ideální váha	18,5 – 25
3	nadváha	25 – 30
4	mírná obezita	30 – 35
5	střední obezita	35 – 40
6	morbidní obezita	> 40

Dokonči funkci, která jako parametry přijímá tělesnou výšku a váhu a vrací odpovídající číslo pásma podle tabulky. Rozmysli (a naprogramuj), co by měla funkce vrátit na rozhraní pásem.

Nápověda

Postupuj obdobně jako v předchozích úlohách. Všimni si, že několikanásobné větvení jsme už naprogramovali pro kvadratickou rovnici. Tam se můžeš inspirovat v tom, jak zdrojový kód uspořádat.

Řešení

Jedno z možných řešení:

 1 def Pasmo(Vaha, Vyska) :
 2     Index = BMI(Vaha, Vyska)	# funkci na vypocet BMI uz mame, tak nebudeme vzorec zadavat znova
 3     if Index <= 16.5 :
 4         return 0
 5     elif Index <= 18.5 :
 6         return 1
 7     elif Index <= 25 :
 8         return 2
 9     elif Index <= 30 :
10         return 3
11     elif Index <= 35 :
12         return 4
13     elif Index <= 40 :
14         return 5
15     else:
16         return 6

Pečliví testeři otestují každé pásmo, především pak pásma krajní, pásma nejvíc využitá v praxi, a rozhraní mezi pásmy.

Vypisování čísla, jehož význam je třeba dohledat v tabulce, jistě není vzorem uživatelské přívětivosti. Jestli chceš zjistit, jak program vylepšit a vypisovat slova, pokračuj do další kapitoly.

Shrnutí

• Má-li program podle různých podmínek postupovat různě, rozvětvíme ho pomocí klíčových slov if, elif a else.
• Příkazy ve větviodsazené příkazy if (či elif) program provede pouze v případě, že bude splněna zadaná podmínka. Naopak větev else se provede, pokud předchozí podmínky splněny nejsou.
• Jednoduchým rovnítkem (=) označujeme přiřazení. Určujeme v něm, jaké hodnoty bude nabývat nějaká proměnná. Výsledkem je přepsaná hodnota proměnné v paměti počítače.
• Dvojitým rovnítkem == označujeme porovnání. Pomocí něj zjišťujeme, jestli se dvě hodnoty rovnají. Výsledkem je odpovídající logická hodnota True nebo False, kterou lze použít např. v rozhodování if.
• Podobně fungují další operátory porovnání: nerovnost (!=) i ostré a neostré větší a menší >, >=, <, <=).
• Tak jako číselné výrazy spojujeme číselnými operacemi, logické výrazy spojujeme operacemi logickými (and, or a not).

Úlohy

Zatím jen stručné náměty. Naprogramuj funkci, která:

• vrátí největší ze tří čísel (zkus najít aspoň dva způsoby řešení; porovnej svoje řešení se spolužáky)
• rozhodne (vrátí True nabo False), jestli je den s daným pořadovým číslem v týdnu pracovní (tedy 1-5, nikoliv 6-7)
• vrátí počet dnů zadaného měsíce
• rozhodne, jestli dané tři délky mohou tvořit strany trojúhelníka
• rozhodne, jakého druhu je trojúhelník o daných stranách (ostro-pravo-tupoúhlý, rovnostranný, rovnoramenný, obecný...)
• rozhodne, jestli je daný rok přestupný (v jakém rozsahu let tvoje funkce funguje správně?)